Khối trụ (trong bài viết này tôi sẽ viết tắt khối trụ là KT) viết là một hình học không gian quen thuộc, xuất hiện trong nhiều khía cạnh của cuộc sống, từ những lon nước giải khát đến các cột trụ trong kiến trúc. Do đó, hiểu rõ về KT, đặc biệt là cách tính thể tích và diện tích của nó, không chỉ giúp chúng ta giải quyết các bài toán hình học mà còn ứng dụng vào thực tiễn. Vậy thế nào là một KT? Bạn đọc hãy cùng KidsUP tìm hiểu về dạng hình học không gian cơ bản này trong bài viết dưới đây nhé!
Định nghĩa Và các đặc điểm cơ bản của khối trụ
Trong toán học, khối trụ, hay còn gọi là hình trụ, là một hình học không gian ba chiều được tạo thành từ hai đáy là hai hình tròn song song và bằng nhau, kết nối bởi một mặt xung quanh là một hình chữ nhật được uốn cong. Khi tính toán một hình trụ, chúng ta có những chỉ số chính sau:

- Bán kính đáy (r): Khoảng cách từ tâm của hình tròn đáy đến bất kỳ điểm nào trên đường tròn.
- Chiều cao (h): Khoảng cách giữa hai đáy hình tròn.
- Đường sinh (l): Đoạn thẳng nối hai điểm tương ứng trên hai đường tròn đáy, và có độ dài bằng chiều cao của KT.
Các Công Thức Cơ Bản Để Tính Khối Trụ
Khối trụ được ứng dụng rất nhiều trong đời sống hàng ngày, vậy nên ta cần phải nắm vững các công thức tính toán liên quan đến KT. Những công thức này sẽ giúp bạn có thể giải các bài toán hình học một cách nhanh chóng và chính xác.

Công thức tính thể tích của khối trụ
V = πr²h
Trong đó:
- V là thể tích của KT.
- π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159.
- r là bán kính đáy của KT.
- h là chiều cao của KT.
Sau đây là một dạng bài tập mẫu về tính thể tích KT:
Một KT có bán kính đáy là 5cm và chiều cao là 10cm, thì thể tích của nó sẽ là:
Giải: Ta có thể tích khối trụ như sau: V = π(5cm)²(10cm) ≈ 785.4 cm³
Công Thức Tính Diện Tích Mặt Ngoài Của Khối Trụ
Cung như bao hình khối không gian khác, ta cần tính cả diện tích xung quanh và diện tích toàn phần của KT. Để tính được hai chỉ số này của một KT, ta có các công thức sau:
- Diện tích xung quanh của KT được tính bằng công thức Sxq = 2πrh.
- Diện tích toàn phần của KT được tính bằng công thức Stp = 2πr(r + h).
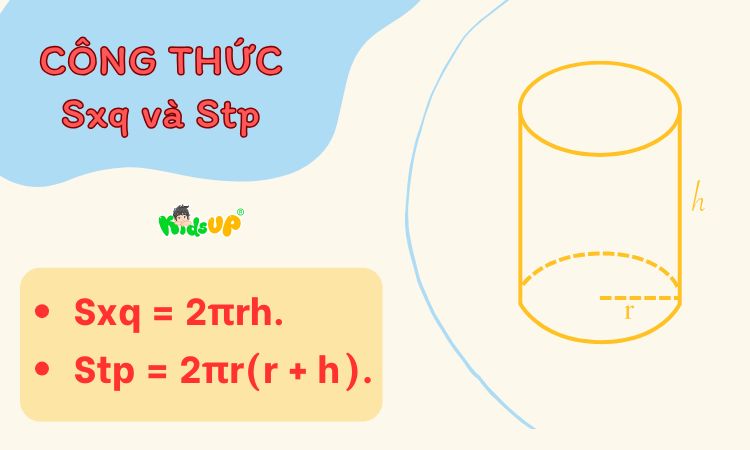
– Một dạng bài tập mẫu về tính diện tích của khối trụ như sau:
KT có bán kính đáy là 5cm và chiều cao là 10cm, hãy tính diện tích xung quanh và diện tích toàn phần của KT.
Giải:
- Diện tích xung quanh là:
- Sxq = 2π(5cm)(10cm) ≈ 314.16 cm²
- Diện tích toàn phần là:
- Stp = 2π(5cm)(5cm + 10cm) ≈ 471.24 cm²
Các Lỗi Thường Gặp Khi Tính Thể Tích và Diện Tích Khối Trụ
Mặc dù công thức tính thể tích và diện tích khối trụ không quá phức tạp, nhưng nhiều học sinh vẫn gặp sai sót trong quá trình tính toán. Những lỗi này chủ yếu đến từ việc nhớ sai công thức, nhầm lẫn giữa bán kính và đường kính hoặc nhập sai dữ liệu vào bài toán.

Lỗi Trong Việc Áp Dụng Công Thức
– Lỗi này thường xảy ra do nhầm lẫn giữa các công thức khác nhau, ví dụ:
- Nhầm lẫn giữa công thức tính Sxq và Stp.
- Quên bình phương bán kính khi tính thể tích.
– Cách khắc phục: Kiểm tra kỹ công thức và số liệu trước khi áp dụng.
– Các phương pháp học tập hiệu quả để củng cố kiến thức bao gồm:
- Sử dụng sơ đồ tư duy.
- Dùng thẻ ghi nhớ.
- Làm nhiều bài tập thực hành.
Lỗi Trong Việc Tính Sai Kích Thước Đường Kính Hoặc Chiều Cao
– Lỗi này có thể xảy ra do:
- Đọc nhầm số liệu.
- Sử dụng sai đơn vị đo
– Cách khắc phục: Tập thói quen ghi chú rõ ràng các số liệu và đơn vị đo để tránh nhầm lẫn.
Bài Tập Thực Hành Để Nâng Cao Kỹ Năng Tính Khối Trụ
– Bài Tập áp dụng công thức thể tích KT
Những bài tập này sẽ giúp bạn làm quen với việc áp dụng công thức tính thể tích KT (V = πr²h). Người học có thể bắt đầu làm quen với cách tính thể tích từ các bài tập đơn giản, sau đó tăng dần độ khó để thử thách bản thân. Sau đây là một vài dạng bài tập mẫu về cách tính thể tích của KT:
Bài tập 1: Một KT có bán kính đáy là 3cm và chiều cao là 7cm. Tính thể tích của KT.
- Đáp án: V = π(3cm)²(7cm) ≈ 197.92 cm³
Bài tập 2: Một khối trụ có đường kính đáy là 10cm và chiều cao là 15cm. Tính thể tích của khối trụ.
- Đáp án: trước tiên ta cần tính bán kính đáy của hình trụ đó là 10cm/2=5cm. sau đó áp dụng công thức tính thể tích hình trụ ta sẽ có V= π(5cm)²(15cm) ≈ 1178.1 cm³
Bài tập 3: Một khối trụ có thể tích là 628 cm³ và chiều cao là 8cm. Tìm bán kính đáy của khối trụ.
- Đáp án: r = √(V / (πh)) = √(628 cm³ / (π * 8cm)) ≈ 5cm
– Bài Tập Tính Diện Tích Khối Trụ
Dạng bài tập này giúp bạn làm quen với việc áp dụng công thức tính diện tích xung quanh (Sxq = 2πrh) và diện tích toàn phần (Stp = 2πr(r + h)) của khối trụ. Thực hành tính toán thông qua những dạng bài tập mẫu sau sẽ giúp bạn nắm vững sự khác biệt giữa hai công thức và áp dụng chúng một cách hiệu quả.
Bài tập 1: Một khối trụ có bán kính đáy là 4cm và chiều cao là 9cm. Tìm Sxq và Stp của khối trụ.
- Đáp án: Sxq = 2π(4cm)(9cm) ≈ 226.19 cm², Stp = 2π(4cm)(4cm + 9cm) ≈ 326.73 cm²
Bài tập 2: Một khối trụ có diện tích xung quanh là 10π cm² và diện tích toàn phần là 18π cm². Tính bán kính đáy và chiều cao của khối trụ.
- Đáp án: r = 2.5cm, h=2cm.
Những Câu Hỏi Thường Gặp Về Khối Trụ và Cách Tính
Câu hỏi 1: Khối Trụ Có Bao Nhiêu Mặt?
Khối trụ có ba mặt:
- Hai mặt đáy là hai hình tròn song song và bằng nhau.
- Một mặt xung quanh là một hình chữ nhật được uốn cong.
Khi mặt xung quanh được trải phẳng ra, nó sẽ tạo thành một hình chữ nhật:
- Chiều dài của hình chữ nhật bằng chu vi của đường tròn đáy.
- Chiều rộng của hình chữ nhật bằng chiều cao của khối trụ.

Câu hỏi 2: Làm Thế Nào Để Tính Thể Tích Khi Không Biết Chiều Cao?
Nếu không biết chiều cao, bạn cần dựa vào những thông tin khác trong đề bài để tính toán.
Ví dụ:
- Nếu biết diện tích xung quanh (Sxq) và bán kính đáy (r), bạn có thể tính chiều cao (h) từ công thức: Sxq=2πrhSxq = 2\pi rhSxq=2πrh
- Sau đó, bạn áp dụng công thức: V=πr2hV = \pi r^2 hV=πr2h để tính thể tích.
- Nếu biết diện tích toàn phần (Stp) và bán kính đáy (r), bạn cũng có thể tính chiều cao (h) và sau đó tính thể tích tương tự.
Việc linh hoạt sử dụng các công thức và thông tin đã biết là chìa khóa để giải quyết các bài toán về khối trụ.
Kết Luận
Bài viết trên là những chia sẻ của KidsUP về khối trụ cùng với những kiến thức liên quan. Hy vọng thông qua những thông tin trên, bạn có thể áp dụng các công thức tính hình trụ thành thạo và linh hoạt. Hẹn gặp lại các bạn đọc trong những bài viết sau trên trang chủ của KidsUP để có thêm nhiều kiến thức thú vị hơn nữa nhé!













