Trong hành trình học toán hình học không gian, khối lăng trụ (viết tắt là: KLT) luôn là một chủ đề quan trọng, tạo nền tảng để hiểu sâu hơn các hình khối phức tạp hơn. KLT xuất hiện không chỉ trong các bài toán lý thuyết mà còn hiện hữu trong đời sống thực tế. Vậy thế nào là một KLT? Các bạn hãy cùng KidsUP tìm hiểu kĩ hơn về khối hình học không gian này trong bài viết dưới đây!
Giới Thiệu Về Khối Lăng Trụ
Khối lăng trụ là một khối hình học có mặt đáy là một đa giác và các mặt bên là các hình chữ nhật. Các mặt đáy của KLT song song với nhau và có hình dạng giống hệt nhau. KLT có thể được phân loại dựa trên hình dạng của mặt đáy, ví dụ như lăng trụ tam giác, lăng trụ vuông, lăng trụ chữ nhật,…

Các Đặc Điểm Cơ Bản Của Khối Lăng Trụ
- Mặt đáy: Là đa giác (ví dụ tam giác, vuông, chữ nhật) có 2 mặt đáy song song và đều giống nhau.
- Mặt bên: Là các hình chữ nhật (hoặc hình vuông) nối các cạnh của mặt đáy.
- Chiều cao: Là khoảng cách giữa hai mặt đáy song song.
- Diện tích toàn phần: Được tính bằng tổng diện tích các mặt đáy và các mặt bên của KLT
Công Thức Tính Toán Khối Lăng Trụ
Để hiểu rõ hơn về KLT và ứng dụng của nó trong thực tế, học sinh cần nắm vững các công thức tính toán liên quan đến dạng hình khối này. Các công thức này giúp chúng ta xác định thể tích, diện tích xung quanh và diện tích toàn phần của KLT, từ đó áp dụng vào giải quyết các bài toán và tình huống thực tế một cách hiệu quả.
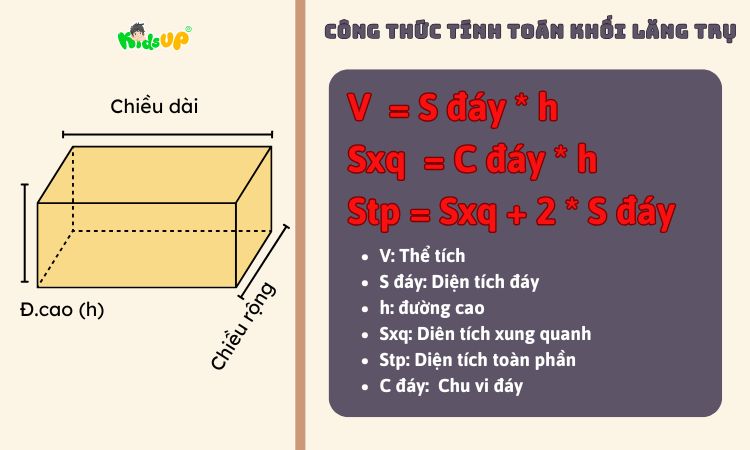
Công Thức Tính Thể Tích Khối Lăng Trụ
Đối với các hình khối không gian trong toán học, công thức tính thể tích là một trong những công thức cơ bản mà người học cần phải nắm vững. Để tính thể tích KLT, ta sẽ có công thức như sau:
V = S đáy * h
Trong đó:
- V là thể tích của KLT.
- S đáy là diện tích của mặt đáy.
- h là chiều cao của KLT (khoảng cách giữa hai mặt đáy).
Ví dụ bài tập: Một KLT đứng có đáy là hình chữ nhật với chiều dài 8cm và chiều rộng 5cm, chiều cao của khối lăng trụ là 10cm. Tính thể tích của KLT đó.
Giải: Diện tích đáy là 8cm * 5cm = 40cm². Thể tích của khối lăng trụ là 40cm² * 10cm = 400cm³.
Công Thức Tính Diện Tích Mặt Xung Quanh Khối Lăng Trụ
Ngoài công thức tính thể tích, công thức tính diện tích xung quanh cũng là một trong những phần kiến thức cơ bản khi nói về hình học không gian. Diện tích xung quanh là tổng diện tích của các bề mặt trong KLT. Để tính diện tích xung quanh của KLT, ta có công thức như sau:
Sxq = C đáy * h
Trong đó:
- Sxq là diện tích mặt xung quanh.
- C đáy là chu vi của mặt đáy.
- h là chiều cao của KLT.
Ví dụ bài tập: Một KLT đứng có đáy là hình tam giác đều cạnh 6cm và chiều cao 8cm. Tính diện tích xung quanh của KLT đó.
Giải: Chu vi đáy là 6cm * 3 = 18cm. Diện tích xung quanh là 18cm * 8cm = 144cm².
Công Thức Tính Diện Tích Toàn Phần Của Khối Lăng Trụ
Ngoài diện tích xung quanh, bạn cũng cần nắm vững công thức này để tính hoàn toàn diện tích của KLT. Diện tích toàn phần của KLT là tổng của diện tích mặt xung quanh và diện tích hai mặt đáy:
Stp = Sxq + 2 * S đáy
Trong đó:
- Stp là diện tích toàn phần.
- Sxq là diện tích mặt xung quanh.
- S đáy là diện tích mặt đáy.
Ví dụ từ trên: Sử dụng số liệu từ ví dụ trên, ta sẽ có bài tập mẫu áp dụng công thức tính diện tích toàn phần của KLT như sau:
Giải: Diện tích đáy là (6² * √3) / 4 ≈ 15.59 cm². Diện tích toàn phần là 144cm² + 2 * 15.59cm² ≈ 175.18cm².
Ứng Dụng Của Khối Lăng Trụ Trong Đời Sống
KLT không chỉ là hình học lý thuyết mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực thực tiễn. Từ xây dựng công trình đến thiết kế sản phẩm, KLT đóng vai trò là một trong những khối cơ bản để mô phỏng, tính toán và thiết kế. Hiểu rõ ứng dụng của KLT sẽ giúp học sinh liên hệ toán học với cuộc sống, tăng cường khả năng tư duy sáng tạo và thực tế.
Ứng Dụng 1: Trong Kiến Trúc và Xây Dựng
Trong lĩnh vực kiến trúc và xây dựng, KLT đóng vai trò then chốt trong việc thiết kế và xây dựng các công trình. Ví dụ, các tòa nhà cao tầng thường được thiết kế theo dạng KLT đứng để đảm bảo tính vững chắc và khả năng chịu lực tốt. Các cột trụ, dầm nhà và mái nhà cũng thường có dạng KLT để tối ưu hóa khả năng chịu tải và phân bổ lực. Ngoài ra, KLT còn được sử dụng để thiết kế các không gian nội thất, tạo nên sự hài hòa và cân đối cho tổng thể công trình.

Ứng Dụng 2: Trong Kỹ Thuật và Cơ Khí
Ngoài lĩnh vực kiến trúc, KLT còn được ứng dụng rất nhiều trong lĩnh vực kĩ thuật và cơ khí. Bạn có thể dễ dàng thấy ứng dụng của KLT trong thiết kế và chế tạo các bộ phận máy móc, đường ống và các cấu trúc khác. Chẳng hạn như các bộ phận máy móc như trục, bánh răng và vỏ máy thường được thiết kế dựa trên nguyên lý KLT để đảm bảo độ chính xác và khả năng hoạt động ổn định.
Ứng Dụng 3: Trong Thiết Kế Đồ Họa và Vật Dụng Hàng Ngày
Trong lĩnh vực thiết kế đồ họa và sản xuất vật dụng hàng ngày, KLT được sử dụng để tạo ra các sản phẩm có tính thẩm mỹ và tiện dụng cao. Ví dụ, các hộp đựng sản phẩm, hộp quà tặng và đồ nội thất thường được thiết kế theo dạng KLT chữ nhật hoặc KLT tam giác để tối ưu hóa không gian và tạo nên sự đẹp mắt. Ngoài ra, KLT còn được sử dụng trong thiết kế đồ họa 3D để tạo ra các mô hình và hiệu ứng hình ảnh sống động.
Lý Thuyết Đằng Sau Công Thức Khối Lăng Trụ
Ngoài việc học công thức, người học cũng cần nắm vững lý thuyết nằm sau đó. Nắm vững các lý thuyết liên quan sẽ giúp bạn có thể linh hoạt xử lý các tình huống mới và nâng cao khả năng tư duy toán học. Khối lăng trụ là minh chứng rõ ràng cho nguyên tắc hình học không gian gắn chặt với các nguyên lý toán học cơ bản.

Các Nguyên Lý Toán Học Cơ Bản Ứng Dụng Trong Khối Lăng Trụ
Khối lăng trụ được xây dựng dựa trên các nguyên lý cơ bản của hình học không gian, bao gồm khái niệm về diện tích, thể tích và tính song song. Diện tích đáy của KLT được tính dựa trên các công thức diện tích của các đa giác, trong khi thể tích được xác định bằng tích của diện tích đáy và chiều cao. Tính song song của các mặt đáy và cạnh bên đảm bảo rằng KLT có tính chất đồng nhất và ổn định.
Mối Quan Hệ Giữa Khối Lăng Trụ và Các Hình Khối Khác
Trong toán học, khối lăng trụ có mối quan hệ chặt chẽ với các hình khối khác trong không gian. Hình hộp chữ nhật và hình lập phương là các trường hợp đặc biệt của KLT, trong đó các mặt đáy là hình chữ nhật và hình vuông. Khối trụ cũng có thể được xem là một trường hợp đặc biệt của KLT khi số cạnh của đáy tiến tới vô cùng, tạo thành hình tròn. Việc hiểu rõ mối quan hệ này giúp chúng ta có cái nhìn tổng quan về các hình khối không gian và cách chúng liên quan với nhau.
Giải Thích Cách Các Công Thức Được Phát Triển và Ứng Dụng
Các công thức tính toán khối lăng trụ được phát triển dựa trên các định lý và nguyên lý toán học cơ bản. Ví dụ, công thức tính thể tích V = S đáy * h được suy ra từ nguyên lý Cavalieri, cho phép so sánh thể tích của các hình khối có cùng diện tích đáy và chiều cao. Các công thức này không chỉ giúp chúng ta tính toán một cách chính xác mà còn là công cụ hữu ích trong việc thiết kế, xây dựng và giải quyết các vấn đề thực tế liên quan đến khối lăng trụ.
Phân Biệt Khối Lăng Trụ Và Khối Trụ Trong Toán Học
Trong thế giới hình học không gian, khối lăng trụ và khối trụ là hai hình khối có những đặc điểm khá tương đồng. Do đó, người mới học thường hay nhầm lẫn định nghĩa giữa hai dạng hình khối này.
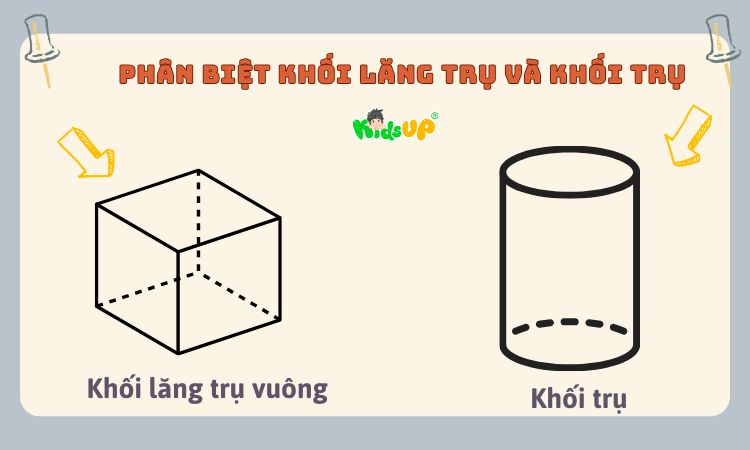
Bảng phân biệt khối lăng trụ và khối trụ
| Đặc điểm | Khối lăng trụ | Khối trụ |
| Mặt đáy | Đa giác (tam giác, tứ giác, ngũ giác,…) | Hình tròn |
| Mặt bên | Hình bình hành | Hình chữ nhật uốn cong |
| Công thức thể tích | V = S đáy * h (S đáy là diện tích đáy, h là chiều cao) | V = πr²h (r là bán kính đáy, h là chiều cao) |
| Ứng dụng | Kiến trúc, xây dựng, thiết kế đồ họa, vật dụng hàng ngày | Đường ống, bình chứa, các chi tiết máy móc hình trụ |
Những Lưu Ý Khi Làm Bài Tập Về Khối Lăng Trụ
Một trong những lỗi phổ biến nhất là nhầm lẫn giữa các công thức tính thể tích, diện tích xung quanh và diện tích toàn phần. Nhiều người học thường áp dụng sai công thức hoặc tính toán sai các đại lượng như diện tích đáy, chu vi đáy và chiều cao. Ngoài ra, Bỏ qua các đơn vị đo hoặc tính toán sai đơn vị cũng là một lỗi thường gặp ở nhiều học sinh.
Để tránh những sai sót khi làm bài tập về khối lăng trụ, người học cần chú ý đến đặc điểm các công thức. Trước khi bắt đầu giải bài, bạn có thể vẽ hình minh họa và ghi chú rõ ràng các kích thước và đơn vị đo. Trong quá trình tính toán, người học cần kiểm tra kỹ các bước và đảm bảo rằng các đơn vị đo được sử dụng một cách nhất quán.
Các Bài Toán Thực Tế Liên Quan Đến Khối Lăng Trụ
Để củng cố kiến thức và rèn luyện kỹ năng giải toán về khối lăng trụ, việc thực hành các bài tập thực tế là rất quan trọng. Các bài tập này không chỉ giúp người học nắm vững công thức mà còn phát triển khả năng tư duy logic và áp dụng kiến thức vào giải quyết các tình huống thực tế.
– Bài Toán Về Tính Thể Tích Khối Lăng Trụ
Ví dụ 1: Một bể cá có dạng khối lăng trụ đứng đáy là hình chữ nhật, chiều dài 1,2m, chiều rộng 0,8m và chiều cao 0,6m. Tính thể tích của bể cá.
Giải: Thể tích bể cá là 1,2m * 0,8m * 0,6m = 0,576m³.
Ví dụ 2: Một khối gỗ có dạng lăng trụ đứng đáy là tam giác vuông, hai cạnh góc vuông lần lượt là 3cm và 4cm, chiều cao của khối gỗ là 10cm. Tính thể tích của khối gỗ.
Giải: Diện tích đáy là (3cm * 4cm) / 2 = 6cm². Thể tích khối gỗ là 6cm² * 10cm = 60cm³
– Bài Toán Tính Diện Tích Mặt Xung Quanh Khối Lăng Trụ
Ví dụ 1: Một cột bê tông có dạng lăng trụ đứng đáy là hình vuông cạnh 50cm, chiều cao cột là 4m. Tính diện tích mặt xung quanh của cột.
Giải: Chu vi đáy cột là 50cm * 4 = 200cm = 2m. Diện tích mặt xung quanh cột là 2m * 4m = 8m².
Ví dụ 2: Tính diện tích mặt xung quanh của khối lăng trụ đứng có đáy là hình thang cân với các cạnh đáy lần lượt là 6cm và 10cm, hai cạnh bên đều bằng 5cm và chiều cao của khối lăng trụ là 8cm.
Giải: Chu vi đáy là 6cm + 10cm + 5cm + 5cm = 26cm. Diện tích xung quanh là 26cm * 8cm = 208cm².
– Cách Giải Quyết Các Bài Toán Khó Về Khối Lăng Trụ
Ví dụ 1: Một khối lăng trụ đứng có đáy là hình thoi với các đường chéo lần lượt là 6cm và 8cm, chiều cao của khối lăng trụ là 12cm. Tính thể tích của khối lăng trụ.
Giải: Diện tích đáy là (6cm * 8cm) / 2 = 24cm². Thể tích khối lăng trụ là 24cm² * 12cm = 288cm³.
Ví dụ 2: Tính diện tích toàn phần của một khối lăng trụ đứng, biết đáy là hình lục giác đều cạnh 4cm và chiều cao là 10cm.
Giải: Diện tích đáy hình lục giác đều là (6 * 4² * √3) / 4 = 24√3 cm². Chu vi đáy là 4cm * 6 = 24cm. Diện tích xung quanh là 24cm * 10cm = 240cm². Diện tích toàn phần là 240cm² + 2 * 24√3 cm².
Kết Luận
Thông qua bài viết trên, KidsUP đã cung cấp cho bạn đọc toàn bộ những thông tin cần biết về khối lăng trụ. Hy vọng những kiến thức trên sẽ giúp các bạn học sinh có thể dễ dàng giải các bài toán liên quan đến khối lăng trụ và áp dụng chúng trong thực tế. Hẹn gặp các bạn ở những bài viết sau của KidsUP để có thêm nhiều kiến thức thú vị hơn nữa nhé!













