Hôm nay, chúng ta sẽ cùng khám phá một hình học vô cùng quen thuộc hình tam giác nhé! Hình tam giác có ba cạnh và ba góc, và ẩn chứa rất nhiều điều thú vị. Khi học về hình tam giác, các bạn sẽ nắm được các tính chất cơ bản, công thức tính chu vi và diện tích nữa. Trong bài viết này, KidsUP sẽ giúp bạn hiểu rõ hơn về hình tam giác, để các bạn tự tin giải các bài toán và áp dụng vào thực tế
Giới thiệu về hình tam giác
Hình tam giác được tạo thành từ ba đoạn thẳng nối ba điểm không thẳng hàng. Những điểm này gọi là ba đỉnh của tam giác. Các đoạn thẳng nối chúng là ba cạnh của tam giác. Tam giác cũng có ba góc tạo thành từ ba cặp cạnh, và tổng ba góc trong của bất kỳ tam giác nào luôn bằng 180 độ.
Phân loại hình tam giác theo độ dài cạnh:
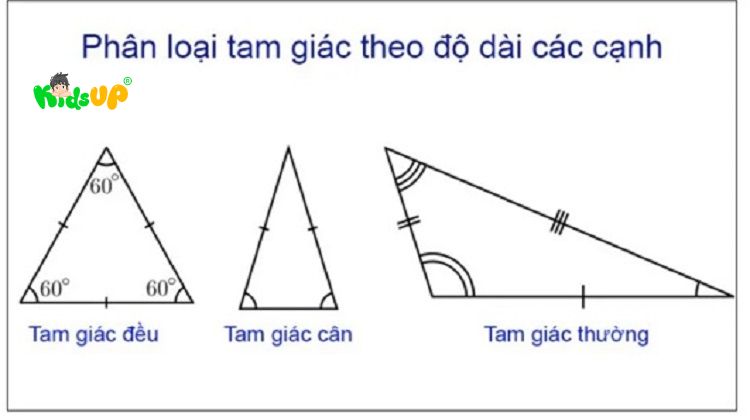
- Tam giác đều: Là tam giác có ba cạnh bằng nhau, đồng thời ba góc cũng bằng nhau, mỗi góc là 60 độ.
- Tam giác cân: Là tam giác có 2 cạnh bằng nhau, trong đó hai góc đối diện với hai cạnh đó cũng bằng nhau.
- Tam giác thường: Là tam giác có ba cạnh không bằng nhau và ba góc cũng khác nhau.
Phân loại hình tam giác theo độ của góc:
- Tam giác vuông: Là tam giác có một góc là 90 độ. Cạnh đối diện với góc 90 độ gọi là cạnh huyền, hai cạnh kế bên còn lại gọi là hai cạnh góc vuông.
- Tam giác tù: Là hình mà có một góc lớn hơn 90 độ.
- Tam giác nhọn: Là hình mà cả ba góc nhỏ đều hơn 90 độ.
Tính chất của hình tam giác
Khi học về hình tam giác, bé cần nắm rõ tính chất của loại hình này. Dưới đây là những tính chất tiêu biểu của hình học này.
Tính chất cạnh và góc của hình tam giác
Trong bất kỳ tam giác nào, tổng của ba góc trong luôn bằng 180 độ. Đây là một tính chất cơ bản và quan trọng của hình tam giác, được áp dụng trong nhiều dạng bài toán và chứng minh.
Trong một tam giác, cạnh lớn nhất sẽ đối diện với góc lớn nhất và cạnh nhỏ nhất sẽ đối diện với góc nhỏ nhất. Điều này nghĩa là, nếu bé biết độ dài của các cạnh, bạn có thể suy luận được góc nào là lớn hay nhỏ. Tương tự, nếu biết được độ lớn của các góc, bé sẽ suy ra thứ tự độ dài của các cạnh.

Tổng độ dài của hai cạnh bất kỳ trong một tam giác sẽ luôn lớn hơn độ dài của cạnh còn lại. Tính chất này còn được gọi là bất đẳng thức tam giác. Đây là một nguyên tắc quan trọng khi xác định độ dài các cạnh trong tam giác.
Cách xác định loại hình tam giác dựa trên độ dài cạnh và góc
Việc phân biệt các loại hình tam giác dựa trên độ dài các cạnh và độ lớn của các góc là một kiến thức hữu ích. Dưới đây là hướng dẫn cụ thể để giúp học sinh nhận diện và phân loại các loại tam giác.
Xác định loại tam giác theo độ dài các cạnh:
- Tam giác đều: Là tam giác có chiều dài ba cạnh bằng nhau. Khi đo các cạnh, nếu tất cả các cạnh có độ dài giống nhau, thì đó là một tam giác đều. Trong tam giác đều, tất cả các góc cũng bằng nhau, mỗi góc đều là 60 độ.
- Tam giác cân: Tam giác cân có hai cạnh bằng nhau và cạnh còn lại có độ dài khác. Nếu khi đo, bạn thấy có hai cạnh bằng nhau, đó là một tam giác cân. Đặc biệt, hai góc đối diện với hai cạnh bằng nhau cũng bằng nhau.
- Tam giác thường: Tam giác thường có ba cạnh với độ dài khác nhau. Nếu đo thấy tất cả các cạnh đều khác nhau, đó là tam giác thường. Trong tam giác thường, không có góc nào và cạnh nào bằng nhau.
Xác định loại tam giác theo góc:
- Tam giác vuông: Là tam giác mà có một góc bằng 90 độ. Để kiểm tra, bé có thể dùng thước đo góc hoặc ê-ke để đo. Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, và đó cũng là cạnh dài nhất của tam giác.
- Tam giác tù: Là hình tam giác sở hữu một góc lớn hơn 90 độ. Khi đo các góc của tam giác, nếu thấy có một góc lớn hơn 90 độ, đó là tam giác tù. Tam giác tù thường có một cạnh dài nhất đối diện với góc tù.
- Tam giác nhọn: Là hình mà cả ba góc đều nhỏ hơn 90 độ. Nếu đo thấy tất cả các góc đều dưới 90 độ, đó là một tam giác nhọn.
Cách tính chu vi hình tam giác
Chu vi của một tam giác được xác định bằng tổng độ dài ba cạnh của tam giác đó. Công thức tính chu vi hình tam giác áp dụng cho mọi loại tam giác, dù là tam giác đều, tam giác cân, tam giác vuông, hay tam giác thường.
Giả sử một tam giác có ba cạnh là b, a và c. Khi đó, chu vi của tam giác được tính theo công thức: P = a + b + c
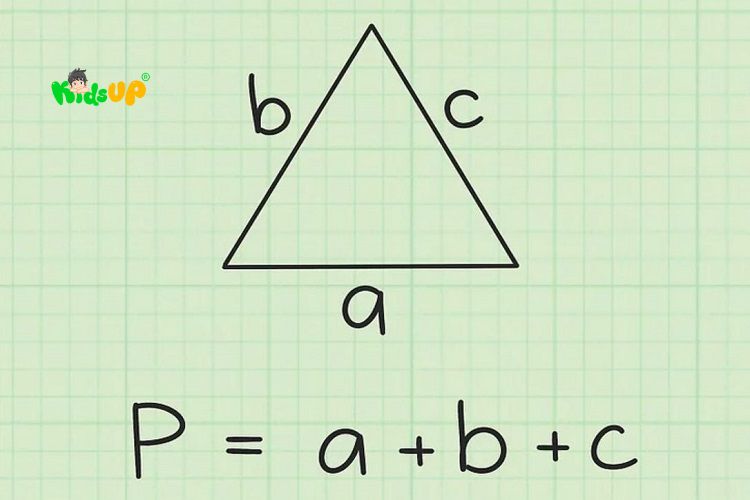
Bài tập thực hành chu vi hình tam giác:
Bài 1: Tam giác ABC có ba cạnh a = 6cm, b = 7cm, c = 9 cm. Hãy tính chu vi tam giác.
Bài 2: Một tam giác đều có cạnh dài 9 cm. Tính chu vi của tam giác này.
Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất dài 6 cm, cạnh góc vuông thứ hai dài 8 cm, và cạnh huyền dài 10 cm. Tính chu vi của tam giác này.
Lời giải:
Bài 1: Chu vi tam giác là: 6 + 7 + 9 = 22 (cm)
Bài 2: Chu vi tam giác là: 9 x 3 = 27 (cm)
Bài 3: Chu vi tam giác là: 6 + 8 + 10 = 24 (cm)
Công thức tính diện tích hình tam giác
Diện tích của một tam giác là phần không gian được bao quanh bởi ba cạnh của tam giác đó. Có nhiều cách tính diện tích tùy vào loại tam giác và thông tin cho trước.
Đối với một hình tam giác bất kỳ, công thức tính diện tích sẽ là: S = 12 x h x a
Trong đó:
- S: Diện tích tam giác
- A: Chiều dài của cạnh đáy
- H: Chiều cao từ đỉnh đến đáy
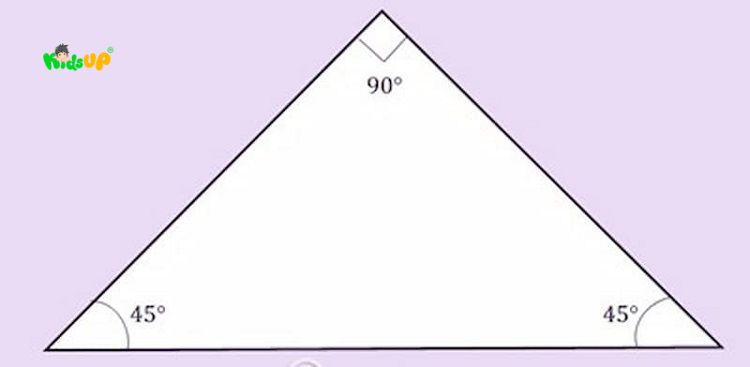
Trường hợp đặc biệt:
Diện tích tam giác đều: Với tam giác đều có độ dài cạnh là a, diện tích được tính bằng công thức: S = 34x a2
Diện tích tam giác vuông: Với tam giác vuông có hai cạnh góc vuông là a và b, diện tích có thể được tính bằng công thức: S = 12 x a x b
Bài tập thực hành tính diện tích hình tam giác
Bài 1: Tam giác ABC có cạnh đáy a=10 cm, chiều cao h=5 cm. Tính diện tích tam giác ABC.
Bài 2: Tam giác vuông BCD có hai cạnh góc vuông là 10 và 8. Tính diện tích tam giác BCD.
Lời giải:
Bài 1: Diện tích tam giác là: S = 12 x 10 x 5 = 25 cm2
Bài 2: Diện tích tam giác BCD: S = 12 x 10 x 8 = 40 cm2
Kết luận
Bài viết trên đã chia sẻ với bạn những công thức quan trọng khi tính hình tam giác. Đây là một trong những hình học cơ bản mà các bé cần nắm vững để làm các bài toán nâng cao về sau. Hy vọng rằng với những chia sẻ từ KidsUP, bạn sẽ giúp bé học kiến thức hình học vững vàng hơn nhé!













