Bạn đã từng “đau đầu” với những bài toán hàm số lũy thừa phức tạp? Đừng lo! Trong bài viết này của KidsUP, chúng tôi sẽ giúp bạn hiểu rõ hàm số lũy thừa là gì và bật mí cách giải nhanh gọn chỉ trong vài bước đơn giản. Với hướng dẫn dễ hiểu, phương pháp nhớ lâu, học sinh sẽ tự tin chinh phục mọi dạng bài từ cơ bản đến nâng cao!
Định nghĩa và tính chất quan trọng của hàm số lũy thừa
Hàm số lũy thừa đóng vai trò quan trọng trong chương trình toán học, không chỉ xuất hiện trong các bài tập cơ bản mà còn liên quan đến nhiều ứng dụng thực tiễn. Việc nắm chắc định nghĩa, tính chất và đồ thị của hàm số này sẽ giúp học sinh giải bài nhanh hơn và hiểu sâu bản chất các dạng toán phức tạp.
Định nghĩa chính xác hàm số lũy thừa
Hàm số lũy thừa là hàm có dạng y = x^n, trong đó n là một số thực bất kỳ. Đối với các giá trị khác nhau của n, đồ thị và tính chất của hàm số sẽ thay đổi, đòi hỏi người học cần nắm vững để vận dụng linh hoạt trong bài tập.

Các tính chất cơ bản cần nhớ
– Tập xác định
- Nếu n là số nguyên dương: Tập xác định là ℝ (tập hợp các số thực).
- Nếu n là số nguyên âm: Tập xác định là ℝ \ {0} (loại bỏ x = 0).
- Nếu n là phân số với mẫu lẻ: Tập xác định thường là [0; +∞) hoặc (0; +∞).
– Tính chất biến thiên trong hàm số lũy từh]à
- Nếu n > 0: Hàm số đồng biến trên khoảng xác định.
- Nếu n < 0: Hàm số nghịch biến trên khoảng xác định.
– Tính chẵn lẻ
- Nếu n chẵn: Hàm số chẵn, đồng nghĩa với f(-x) = f(x).
- Nếu n lẻ: Hàm số lẻ, đồng nghĩa với f(-x) = -f(x).
– Giới hạn và tính liên tục
- Hàm số lũy thừa liên tục trên tập xác định của nó.
- Giới hạn tại điểm xốc (đặc biệt x tiến đến 0 hoặc +∞, -∞) được xác định tùy vào giá trị của n.
Cách vẽ đồ thị hàm số lũy thừa cực nhanh
Đồ thị hàm số lũy thừa có nhiều dạng đặc trưng khác nhau tùy vào giá trị của số mũ. Nếu nắm chắc các bước cơ bản và mẹo nhìn nhanh, học sinh có thể vẽ chuẩn đồ thị chỉ trong vài phút mà không cần giải chi tiết rườm rà.
Bước 1: Xác định dạng của hàm số
Trước tiên, xác định xem hàm số có dạng y = x^n với n nguyên dương, nguyên âm, hay phân số. Từ đó dự đoán sơ bộ về hình dạng đồ thị: đối xứng, tiệm cận, hướng đi lên hay đi xuống.
Bước 2: Tìm tập xác định và bảng biến thiên
- Tập xác định: Xem xét kỹ xem hàm số có loại bỏ giá trị nào không (thường là x = 0 với n âm hoặc số lẻ).
- Bảng biến thiên: Xác định khoảng đồng biến hoặc nghịch biến, các giá trị đặc biệt (x = 0, x = 1, x = -1).
Bước 3: Các mẹo “nhìn nhanh” đồ thị mà không cần giải chi tiết
- Nếu n chẵn và dương: đồ thị hình chữ U, nằm phía trên trục hoành, đối xứng qua trục tung.
- Nếu n lẻ và dương: đồ thị đi qua gốc tọa độ, hướng từ góc trái dưới lên góc phải trên.
- Nếu n âm: đồ thị tiệm cận đứng (x = 0) và tiệm cận ngang (y = 0).
- Ưu tiên xét nhanh tại các điểm x = -1, 0, 1 để phác thảo hình dạng cơ bản.
– Những lỗi thường gặp khi vẽ và cách tránh
- Nhầm tập xác định: Quên loại trừ x = 0 đối với n âm. => Luôn kiểm tra kỹ trước khi vẽ.
- Nhầm tính đối xứng: Không phân biệt hàm chẵn (đối xứng trục tung) và hàm lẻ (đối xứng gốc tọa độ). => Xác định tính chẵn/lẻ trước khi vẽ.
- Vẽ sai hướng đồ thị: Đặc biệt với n âm, dễ bị nhầm chiều tiệm cận. => Ghi nhớ quy luật: n âm, đồ thị tiến gần tiệm cận.
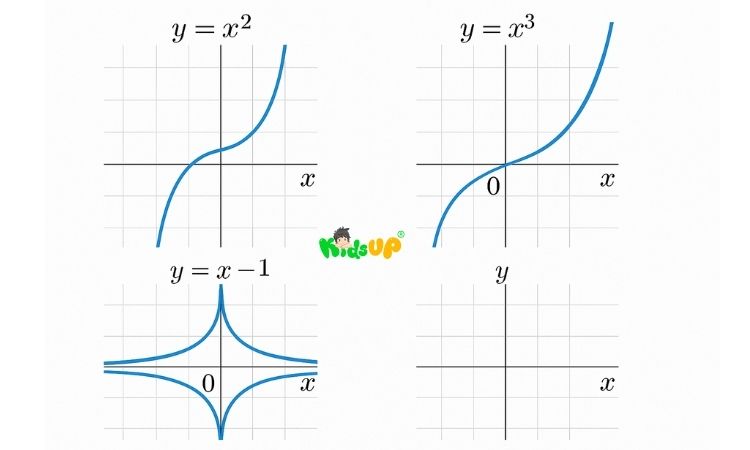
– Ví dụ minh họa bằng hình ảnh đồ thị
- y = x^2 (n = 2): Hình chữ U hướng lên.
- y = x^3 (n = 3): Đường cong đi qua gốc tọa độ, xuôi chiều từ dưới lên.
- y = x^{-1} (n = -1): Hai nhánh đối xứng qua gốc tọa độ, có tiệm cận x = 0 và y = 0.
Công thức cần nhớ và ứng dụng vào giải bài tập
Tổng hợp công thức rút gọn hàm số lũy thừa
- Nhân lũy thừa cùng cơ số: x^m × x^n = x^(m+n)
- Chia lũy thừa cùng cơ số: x^m / x^n = x^(m-n) (với x ≠ 0)
- Lũy thừa của lũy thừa: (x^m)^n = x^(m×n)
- Lũy thừa của một tích: (xy)^n = x^n × y^n
- Lũy thừa của một thương: (x/y)^n = x^n / y^n (với y ≠ 0)
Ví dụ 1: Rút gọn biểu thức: A = x^3 × x^(-2) × (x^2)^3
Hướng dẫn chi tiết:
- Áp dụng công thức nhân lũy thừa cùng cơ số: x^3 × x^(-2) = x^(3-2) = x^1 = x
- Áp dụng công thức lũy thừa của lũy thừa: (x^2)^3 = x^(2×3) = x^6
- Nhân tiếp: x × x^6 = x^(1+6) = x^7
Kết quả: A = x^7
Ví dụ 2: Tìm tập xác định và vẽ sơ đồ biến thiên của hàm số y = x^(-2).
Hướng dẫn chi tiết:
- Tập xác định: Hàm số không xác định tại x = 0. Vậy tập xác định là R \ {0}.
- Biến thiên: Vì số mũ âm, hàm số nghịch biến trên từng khoảng xác định.
- Hình dạng đồ thị: Đồ thị gồm 2 nhánh, mỗi nhánh nằm ở góc phần tư I và II, tiệm cận đứng tại x = 0 và tiệm cận ngang tại y = 0
Bảng tổng hợp công thức rút gọn hàm số lũy thừa
| Công thức | Ý nghĩa |
| xm × xn = xm+n | Nhân lũy thừa cùng cơ số |
| xm ÷ xn = xm-n (với x ≠ 0) | Chia lũy thừa cùng cơ số |
| (xm)n = xm×n | Lũy thừa của lũy thừa |
| (xy)n = xn × yn | Lũy thừa của một tích |
| (x/y)n = xn ÷ yn (với y ≠ 0) | Lũy thừa của một thương |
Mẹo học và ghi nhớ hàm số lũy thừa cho học sinh
Để học tốt hàm số lũy thừa, ngoài việc nắm chắc lý thuyết cơ bản, học sinh cần trang bị thêm các mẹo nhận diện nhanh, ghi nhớ công thức dễ dàng và tránh các lỗi phổ biến thường gặp trong quá trình làm bài.
– Cách phân biệt các dạng bài nhanh chóng
- Nhận diện qua số mũ: Nếu số mũ nguyên dương ⇒ dạng cơ bản dễ vẽ đồ thị; nếu số mũ âm hoặc phân số ⇒ cần chú ý tập xác định và tiệm cận.
- Kiểm tra yêu cầu đề bài: Nếu đề bài hỏi về tính đơn điệu (đồng biến, nghịch biến) ⇒ tập trung xét đạo hàm nhanh; nếu hỏi đồ thị ⇒ xác định tính chẵn lẻ trước.
- Chú ý dấu hiệu đặc trưng: Các hàm số có lũy thừa âm thường có tiệm cận, các hàm số lũy thừa chẵn có đồ thị dạng chữ U.
– Bí quyết làm bài thi trắc nghiệm “siêu tốc”
- Ghi nhớ mô hình đồ thị mẫu: Chỉ cần nhớ 3 dạng chính (n chẵn, n lẻ, n âm) để loại nhanh đáp án sai.
- Sử dụng quy tắc dấu nhanh: Nhẩm nhanh dấu đạo hàm để suy ra đồng biến/nghịch biến mà không cần giải đạo hàm chi tiết.
- Tận dụng tính chất đối xứng: Khi đề bài cho bảng biến thiên hay đồ thị, xác định tính chẵn/lẻ giúp chọn đáp án nhanh hơn.
- Ưu tiên kiểm tra các giá trị đặc biệt: Thay nhanh x = 0, x = 1, x = -1 để xác định giá trị y tương ứng, dễ dàng so sánh đáp án.
– Cách tránh những lỗi hay gặp
- Nhầm tập xác định: Đặc biệt với số mũ âm, dễ quên loại x = 0. Cách tránh: Luôn xét tập xác định trước khi làm các bước tiếp theo.
- Nhầm chiều biến thiên: Với số mũ âm, học sinh hay nhầm đồng biến thành nghịch biến. Cách tránh: Ghi nhớ quy tắc: số mũ âm → hàm nghịch biến trên miền dương.
- Vẽ sai hình dạng đồ thị: Không phân biệt n chẵn/n lẻ. Cách tránh: Học thuộc mẫu đồ thị cơ bản rồi suy rộng ra.
- Quên tiệm cận: Đặc biệt với hàm số có n âm, dễ bỏ sót tiệm cận đứng và ngang. Cách tránh: Mỗi khi gặp số mũ âm, tự động xét tiệm cận đầu tiên.
Bài tập tự luyện ở nhà (Có đáp án)
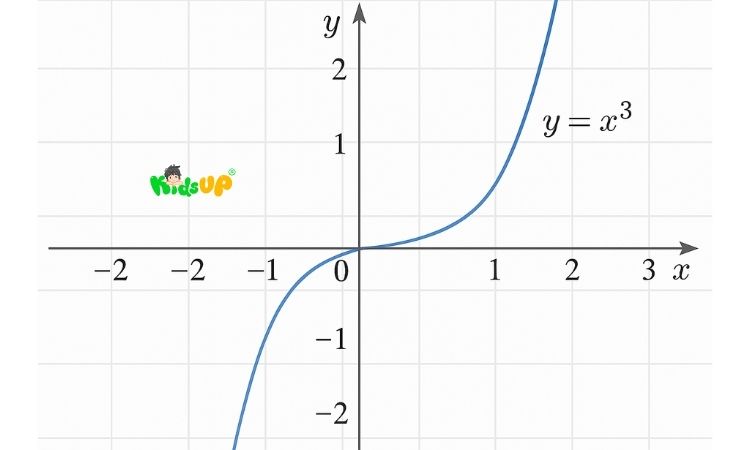
– Bài 1: Cho hàm số y = x³. Vẽ đồ thị và xác định:
- Tính biến thiên của hàm số.
- Tính chẵn lẻ của hàm số.
Đáp án
- Đồ thị: Là một đường cong đi qua gốc tọa độ (0;0), hướng từ góc phần tư III đến góc phần tư I.
- Đồng biến: Hàm số đồng biến trên toàn bộ tập xác định R.
- Tính lẻ: Vì y(-x) = -(y(x)), nên hàm số là hàm lẻ, đối xứng qua gốc tọa độ.
– Bài 2: Cho hàm số y = x-2. Vẽ đồ thị và xác định:
- Tiệm cận đứng và tiệm cận ngang của đồ thị.
- Khoảng biến thiên của đồ thị.
Đáp án
- Đồ thị: Có hai nhánh, nằm ở góc phần tư I và II.
- Tiệm cận đứng: x = 0.
- Tiệm cận ngang: y = 0.
- Biến thiên: Hàm số nghịch biến trên mỗi khoảng (-∞; 0) và (0; +∞).
Kết Luận
Khi nắm vững lý thuyết và áp dụng đúng mẹo học, việc giải bài tập liên quan đến hàm số lũy thừa sẽ trở nên dễ dàng và nhanh chóng hơn bao giờ hết. KidsUP hy vọng rằng với những kiến thức và phương pháp đã chia sẻ, các bạn học sinh sẽ tự tin chinh phục mọi thử thách trong học tập. Cùng KidsUP đồng hành để việc học Toán trở nên thú vị và hiệu quả hơn mỗi ngày!













