Hàm số logarit luôn khiến nhiều học sinh “đau đầu” vì tính chất đặc biệt và cách biến đổi phức tạp. Tuy nhiên, nếu nắm được cách nhận dạng nhanh và áp dụng các mẹo giải bài tập thông minh, bạn hoàn toàn có thể chinh phục dạng toán này dễ dàng. Bài viết dưới đây của KidsUP sẽ bật mí cho bạn những bí quyết cực kỳ hiệu quả để làm chủ hàm số logarit trong thời gian ngắn nhất!
Tổng quan về hàm số logarit
Hàm số logarit là một phần kiến thức quan trọng trong chương trình Toán học, đặc biệt trong các kỳ thi lớn. Để hiểu rõ hơn, chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất cơ bản của hàm logarit, cũng như khám phá hình dạng đồ thị và những điểm đặc biệt của nó so với hàm số mũ.
Khái niệm hàm số logarit
Hàm số logarit cơ bản có dạng y = logax với a > 0 và a ≠ 1. Đây là hàm ngược của hàm số mũ y = ax. Trong đó, logax được hiểu là số mũ mà ta phải nâng cơ số a lên để được x.

Tập xác định và tập giá trị
- Tập xác định: Hàm số logarit chỉ xác định với các giá trị x > 0, nghĩa là tập xác định là (0; +∞).
- Tập giá trị: Giá trị của hàm số logarit có thể nhận bất kỳ số thực nào, tức là tập giá trị là ℝ.
Tính đơn điệu: đồng biến và nghịch biến
- Nếu a > 1, hàm số y = logax đồng biến trên khoảng (0; +∞), tức là x tăng thì y cũng tăng.
- Nếu 0 < a < 1, hàm số y = logax nghịch biến trên khoảng (0; +∞), tức là x tăng thì y giảm.
Đồ thị hàm số logarit
– Hình dạng đồ thị
Đồ thị hàm số y = logax là một đường cong liên tục, đi qua điểm (1; 0) và không cắt trục tung. Hình dạng cụ thể của đồ thị phụ thuộc vào giá trị của cơ số a.
– Tiệm cận và điểm đặc biệt
- Tiệm cận: Đồ thị có tiệm cận đứng là đường thẳng x = 0 (trục tung).
- Điểm đặc biệt: Điểm (1; 0) luôn nằm trên đồ thị vì loga1 = 0 với mọi a > 0, a ≠ 1.
– So sánh với đồ thị hàm số mũ
- Đồ thị hàm số mũ y = ax có trục hoành là tiệm cận, trong khi đồ thị logarit có trục tung là tiệm cận.
- Nếu hàm mũ “vút lên” rất nhanh khi x tăng thì đồ thị logarit lại tăng chậm, thoải dần và “bò” theo trục hoành khi x lớn.
Phân loại bài tập hàm số logarit
Bài tập liên quan đến hàm số logarit khá đa dạng và phong phú, từ nhận dạng đồ thị, giải phương trình, bất phương trình cho đến ứng dụng đạo hàm. Để học hiệu quả, bạn cần nắm chắc cách phân biệt đồ thị, thành thạo các kỹ thuật biến đổi logarit và hiểu rõ cách vận dụng đạo hàm trong khảo sát hàm số. Hãy cùng khám phá chi tiết từng dạng bài ngay sau đây!
Nhận dạng đồ thị hàm số logarit
– Dấu hiệu nhận biết nhanh
Đồ thị hàm số logarit y = logax có đặc điểm điển hình là:
- Đi qua điểm (1; 0).
- Có tiệm cận đứng là trục tung (x = 0).
- Không cắt trục tung và kéo dài về phía bên phải.
Hàm số đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
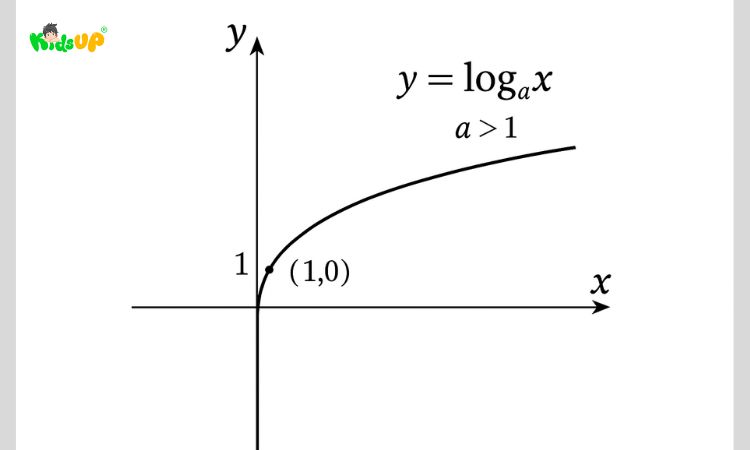
– Mẹo phân biệt với đồ thị hàm số mũ
- Đồ thị hàm số mũ y = ax đi qua điểm (0; 1) và tiệm cận trục hoành (y = 0).
- Đồ thị hàm logarit y = logax đi qua điểm (1; 0) và tiệm cận trục tung (x = 0).
- Nhớ quy tắc: “Mũ bám ngang, log bám đứng”.
Giải phương trình và bất phương trình logarit
– Phương pháp giải cơ bản
Khi giải phương trình logarit, bước đầu tiên là đưa phương trình về dạng cơ bản:
- Biến đổi để hai vế cùng chứa logarit có cùng cơ số.
- Áp dụng điều kiện xác định: các biểu thức bên trong logarit phải dương.
- Sau khi triệt tiêu logarit, giải phương trình bình thường như đại số.
– Sử dụng tính chất logarit để biến đổi
Một số tính chất thường dùng khi giải bài tập:
- loga(xy) = logax + logay
- loga(x/y) = logax – logay
- logaxn = n.logax
Ứng dụng đạo hàm trong hàm số logarit
– Tính đạo hàm của hàm logarit
Hàm logarit với công thức đạo hàm cơ bản là:
- (logax)’ = 1 / (x \ln a)
- (ln x)’ = 1 / x với ln x là logarit tự nhiên cơ số e.
Khi tính đạo hàm của những biểu thức phức tạp, cần vận dụng thêm các quy tắc đạo hàm tổng, hiệu, tích, thương.
– Ứng dụng trong khảo sát hàm số
- Sử dụng đạo hàm để xác định tính đơn điệu (đồng biến, nghịch biến) của hàm logarit.
- Tìm cực trị (cực đại, cực tiểu) của hàm số liên quan đến logarit.
- Khảo sát sự biến thiên, lập bảng biến thiên và vẽ đồ thị hàm số logarit
Mẹo giải nhanh bài tập hàm số logarit
Để làm tốt bài tập hàm số logarit trong thời gian ngắn, ngoài việc nắm chắc kiến thức cơ bản, bạn còn cần những mẹo giải nhanh hiệu quả. Từ việc sử dụng máy tính cầm tay thông minh, vận dụng phương pháp hàm đặc trưng, cho đến kỹ thuật nhận diện đáp án đúng – tất cả sẽ giúp bạn tiết kiệm thời gian và tăng độ chính xác khi làm bài.
Mẹo 1 – Sử dụng máy tính cầm tay hiệu quả
Bấm máy tính Casino để tìm phương trình logarit
Máy tính cầm tay hiện nay hỗ trợ các chức năng logarit rất thuận tiện. Bạn có thể sử dụng phím log để tính logarit cơ số 10 hoặc phím ln để tính logarit tự nhiên. Ngoài ra, với một số dòng máy như Casio fx-570VN Plus, bạn còn có thể dùng tính năng logab để nhập trực tiếp cơ số và số cần tính.

Lưu ý khi sử dụng các hàm logarit trên máy tính
- Luôn kiểm tra lại điều kiện xác định trước khi tính toán.
- Chú ý nhập đúng thứ tự cơ số và số bị lấy log để tránh nhầm lẫn.
- Đối với phương trình, nên sử dụng chức năng SOLVE hoặc table để tìm nghiệm nhanh chóng.
Mẹo 2 – Phương pháp hàm đặc trưng
Giới thiệu phương pháp
Phương pháp hàm đặc trưng là kỹ thuật gán giá trị đặc biệt cho biến số (thường là x = 1 hoặc các giá trị đơn giản) nhằm biến bài toán phức tạp thành bài toán đơn giản hơn, từ đó nhanh chóng xác định đáp án hoặc phương án đúng.
Phù hợp cho dạng bài toán trắc nghiệm
- Khi đề bài cho nhiều biểu thức phức tạp, chọn giá trị x đơn giản để thay vào và so sánh kết quả các đáp án.
- Cách này đặc biệt hiệu quả trong các câu hỏi trắc nghiệm có giới hạn thời gian, giúp bạn khoanh đáp án nhanh chóng mà không cần giải chi tiết.
Mẹo 3 – Nhận diện nhanh đáp án đúng
Mẹo loại trừ đáp án sai
Trong bài trắc nghiệm, nhiều khi không cần giải hết bài mà có thể loại bỏ các đáp án vô lý ngay từ bước đầu. Các dấu hiệu loại trừ thường gặp:
- Đáp án chứa logarit âm hoặc logarit của số âm là loại ngay.
- Đáp án không thỏa điều kiện xác định của hàm logarit.
- Đáp án có dạng quá phức tạp so với yêu cầu bài toán.
Kỹ thuật thử đáp án nhanh chóng
- Thay giá trị đơn giản vào từng đáp án để kiểm tra đúng/sai.
- Ưu tiên thử các giá trị như x = 1, x = 10 hoặc các số dễ tính logarit.
- Nếu nhiều đáp án cùng đúng ở một giá trị, thử thêm giá trị khác để phân biệt chính xác
Bài tập thực hành hàm số Logarit (Có đáp án)
– Bài tập nhận dạng đồ thị
Cho đồ thị hàm số, hãy xác định đó là đồ thị của hàm nào trong các hàm sau:
- A. y = log2x
- B. y = log0.5x
- C. y = 2x
- D. y = 0.5x
Hướng dẫn giải chi tiết
Quan sát đồ thị, nếu:
- Đồ thị có tiệm cận đứng (gần trục tung) và đi qua điểm (1; 0) thì là hàm logarit.
- Đồ thị đồng biến (x tăng, y tăng) thì cơ số a > 1 → chọn A.
- Đồ thị nghịch biến (x tăng, y giảm) thì cơ số 0 < a < 1 → chọn B.
Đáp án đúng tùy thuộc vào chiều biến thiên của đồ thị đã cho.
– Bài tập phương trình logarit
Giải phương trình sau: log2(x – 1) + log2(x + 3) = 3
Hướng dẫn giải chi tiết
Bước 1: Áp dụng công thức: logaA + logaB = loga(A.B)
Phương trình trở thành: log2((x – 1)(x + 3)) = 3
Bước 2: Đưa về dạng cơ bản: (x – 1)(x + 3) = 2³ = 8
Bước 3: Giải phương trình:
x² + 2x – 3 = 8 → x² + 2x – 11 = 0
Giải bằng công thức nghiệm: x = (-2 ± √(4 + 44)) / 2 = (-2 ± √48) / 2 = (-2 ± 4√3) / 2
→ x = -1 + 2√3 hoặc x = -1 – 2√3
Bước 4: Kiểm tra điều kiện:
Chỉ nhận giá trị x sao cho x – 1 > 0 và x + 3 > 0. Vì vậy, loại nghiệm âm.
Kết quả: x = -1 + 2√3.
– Bài tập ứng dụng đạo hàm
Cho hàm số y = log3(2x + 1). Tính đạo hàm của hàm số này.
Hướng dẫn giải chi tiết
Áp dụng công thức đạo hàm: (logau(x))’ = u'(x) / (u(x) ln a)
Ta có:
- u(x) = 2x + 1 ⇒ u'(x) = 2
- ln 3 ≈ 1.0986
Vậy đạo hàm là: y’ = 2 / [(2x + 1) ln 3]
Kết Luận
Hàm số logarit không còn là thử thách nếu bạn áp dụng đúng phương pháp và luyện tập thường xuyên. Cùng KidsUP khám phá thêm nhiều bí quyết học tập thông minh để hành trình chinh phục môn Toán trở nên dễ dàng và thú vị hơn nhé!












