Hình thang là một hình dạng thú vị với cấu trúc đặc biệt, khác hẳn so với hình tam giác hay hình chữ nhật. Việc nắm vững đặc điểm của hình này sẽ giúp bé dễ dàng tính toán chu vi và diện tích. Trong bài viết này, KidsUP sẽ đồng hành cùng bé khám phá toàn bộ kiến thức về hình thang, từ tính chất đến cách tính chu vi và diện tích.
Định nghĩa và các loại hình thang phổ biến
Hình thang là một tứ giác lồi có hai cạnh đối song song và hai cạnh còn lại không song song. Hai cạnh song song này được gọi là hai cạnh đáy (đáy lớn và đáy nhỏ), trong khi hai cạnh còn lại được gọi là hai cạnh bên. Nhờ vào tính chất song song của hai cạnh đáy, hình thang có nhiều đặc điểm độc đáo, khác biệt so với các tứ giác khác.
Các loại hình thang phổ biến:
- Hình thang thường: Chỉ có hai cạnh đối song song mà không có các tính chất đặc biệt khác. Các cạnh bên của hình thường không bằng nhau và không vuông góc với hai cạnh đáy.
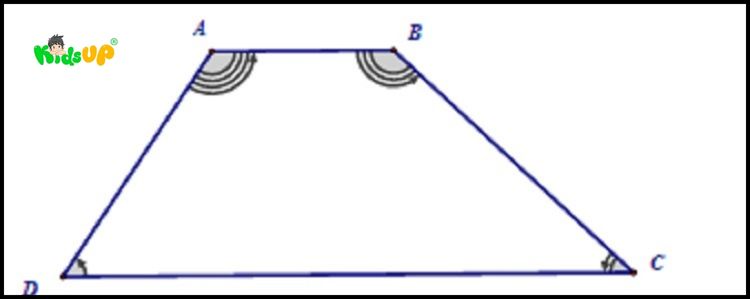
- Hình thang cân: Là loại HÌNH có hai cạnh bên bằng nhau, tạo ra tính đối xứng từ trục đối xứng đi qua trung điểm của hai cạnh đáy. Hình thang cân có tính chất đặc biệt là hai góc ở đáy lớn bằng nhau, và hai góc ở đáy nhỏ cũng bằng nhau.
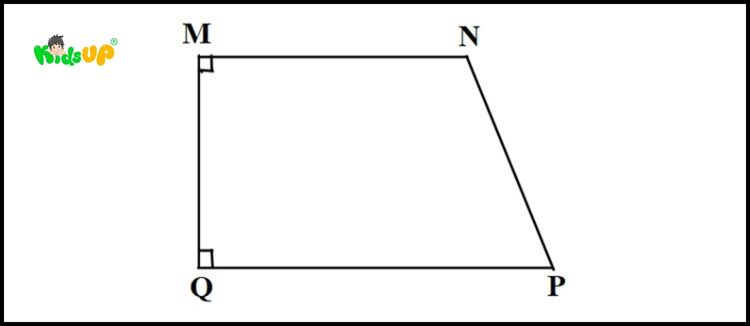
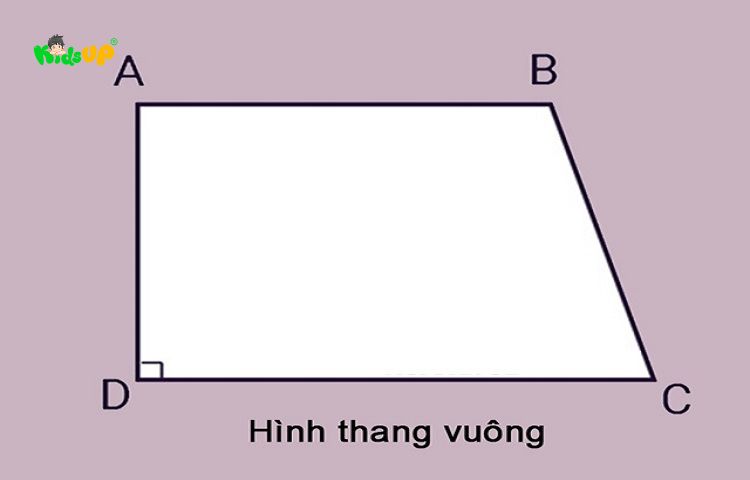
- Hình thang vuông: Là hình sở hữu 1 góc vuông. Cạnh bên vuông góc với hai cạnh đáy, tạo thành hình chữ L hoặc gần giống chữ L.
- Hình bình hành (trường hợp đặc biệt của hình thang): Hình bình hành là một dạng đặc biệt của hình thang, trong đó cả hai cặp cạnh đối song song với nhau.
Tính chất của hình thang
Hình thang có tính chất đặc biệt so với các hình học còn lại. Trẻ cần phải hiểu rõ các tính chất sau để có thể phân biệt thành thêm với các hình còn lại:
Tính chất về cạnh và góc
- Hai cạnh đáy song song: Hình thang có hai cạnh đối song song, gọi là cạnh đáy (đáy lớn và đáy nhỏ).
- Tổng hai góc kề một cạnh bên bằng 180 độ
- Không nhất thiết các cạnh bên phải bằng nhau: Trừ trường hợp hình thang cân, hai cạnh bên của hình thang không cần phải bằng nhau và không nhất thiết vuông góc với hai cạnh đáy.
Tính chất về hai đường chéo
- Không cắt nhau tại trung điểm: Hai đường chéo không cắt nhau tại trung điểm của mỗi đường chéo (khác với hình bình hành). Điểm cắt nhau của hai đường chéo sẽ không chia chúng thành hai đoạn bằng nhau, trừ khi đó là hình thang cân.
- Đường trung bình: Đường thẳng nối trung điểm của hai cạnh bên trong hình thang được gọi là đường trung bình. Đường trung bình có độ dài bằng trung bình cộng của hai cạnh đáy và song song với hai cạnh đáy.
Tính chất của hình thang vuông
- Có một góc vuông: Hình thang vuông là hình thang có một góc vuông (90 độ), tức là một cạnh bên vuông góc với hai cạnh đáy.
- Độ dài cạnh bên: Trong hình thang vuông, cạnh bên vuông góc với hai cạnh đáy có vai trò như chiều cao của hình thang, giúp đơn giản hóa việc tính diện tích.
- Chỉ có một cặp góc vuông: Hình thang vuông có thể có tối đa một cặp góc vuông, và góc vuông này chỉ nằm ở một bên của hình thang.
Tính chất của hình thang cân
- Hai cạnh bên bằng nhau: Trong hình thang cân, hai cạnh bên bằng nhau, tạo nên tính đối xứng cho hình thang.
- Hai góc bằng nhau: Do tính chất đối xứng, hai góc kề đáy lớn bằng nhau và hai góc kề đáy nhỏ cũng bằng nhau.
- Hai đường chéo bằng nhau: Một tính chất đặc biệt của hình thang cân là hai đường chéo bằng nhau, tức là độ dài của hai đường chéo luôn bằng nhau.
- Trục đối xứng: Hình thang cân có một trục đối xứng đi qua trung điểm của hai cạnh đáy, chia hình thang thành hai phần đối xứng.
Công thức tính diện tích và chu vi hình thang
Dưới đây là công thức tính diện tích và chu vi hình thang sẽ giúp trẻ giải các bài toán từ cơ bản đến nâng cao về hình thang.
Công thức tính diện tích hình thang
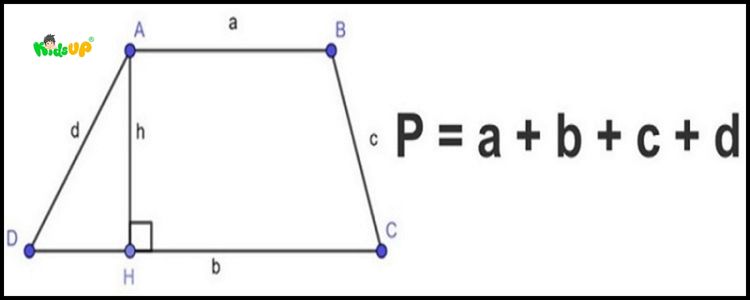
Diện tích của hình thang được tính bằng công thức sau: S = (a + b) x h2
Trong đó:
- a là độ dài của đáy lớn.
- b là độ dài của đáy nhỏ.
- h gọi là chiều cao của hình thang (khoảng cách vuông góc với 2 cạnh đáy).
Công thức chu vi hình thang
Chu vi của hình thang là tổng độ dài của bốn cạnh nên công thức tính chu vi là: P = a + b + c + d
Trong đó:
- a và b là độ dài của hai cạnh đáy trong hình.
- c và d là độ dài của hai cạnh bên trong hình thang.
Giải các bài toán cơ bản về hình thang
Một phương pháp giúp cho bé có thể dễ dàng nhớ các công thức tính hình thang chính là làm bài tập. Bạn có thể hướng dẫn bé tham khảo một số dạng bài tập phổ biến sau đây:
Dạng bài tập tính diện tích
Bài tập 1: Cho hình thang ABCD có: Đáy lớn AB = 14 cm, đáy nhỏ CD = 10 cm, chiều cao h = 6 cm. Tính diện tích hình thang.
Lời giải:
Diện tích hình thang là: S = (a + b) x h2 = (14 + 10) x 62= 72 (cm2)
Bài tập 2:
Cho một hình thang có diện tích là 90 cm2, đáy lớn a = 15 cm, đáy nhỏ b = 9 cm. Tính chiều cao của hình thang.
Lời giải:
Công thức tính diện tích hình thang là: S = (a + b) x h2 => h = 2Sa + b
Chiều cao của hình thang là: h = 2Sa + b = 2 x 9015 + 9 = 18024 = 7.5 (cm)
Dạng bài tập tính chu vi
Bài tập 1: Cho hình thang EFGH với: Đáy lớn EF = 20 cm, đáy nhỏ GH = 12 cm, cạnh bên EG = 9 cm, cạnh bên FH = 7 cm. Tính chu vi của hình thang.
Lời giải: Chu vi hình thang là: P= a + b + c + d = 20 + 12 + 9 + 7 = 48 (cm).

Bài 2: Cho hình thang ABCD, trong đó chu vi là 50 cm, đáy lớn a là 20 cm, hai cạnh bên c và d mỗi cạnh 12 cm. Tìm đáy nhỏ.
Lời giải:
Công thức tính chu vi hình thang là: P= a + b + c + d => b = P – a – c – d
Đáy nhỏ của hình thang là: b = 50 – 20 – 12 – 12 = 6 (cm).
Dạng bài tập về tính chất hình thang
Bài 1: Cho hình thang cân PQRS với: Đáy lớn PQ = 16 cm, đáy nhỏ RS =10 cm, cạnh bên PR = QS = 6 cm. Yêu cầu: Chứng minh rằng PQRS là hình thang cân.
Hình thang PQRS có hai cạnh bên PR và QS bằng nhau (PR=QS=6 cm), nên theo định nghĩa, PQRS là hình thang cân.
Bài 2: Cho hình thang ABCD có đáy lớn AB là 18 cm, đáy nhỏ CD là 12 cm, cạnh bên AC là 8 cm ( vuông góc với đáy). Yêu cầu:
- Chứng minh hình học ABCD là hình thang vuông.
- Tính diện tích ABCD.
Lời giải:
Cạnh bên AC vuông góc với đáy nên ABCD là hình thang vuông.
Vì hình thang vuông nên chiều cao sẽ là cạnh vuông góc với mặt đáy. Từ đó, ta có:
Công thức tính diện tích: S = (a + b) x h2 = (18 + 12) x 82= 120 cm2

Phương pháp giải toán về hình thang
Để giải các bài tập về hình thang, trẻ có thể áp dụng hai phương pháp chính: Sử dụng công thức và lập luận suy luận dựa trên tính chất của hình thang. Bạn có thể tham khảo hai phương pháp giải toán về hình thang sau:
Phương pháp sử dụng công thức
Phương pháp này thường được áp dụng khi bài toán yêu cầu tính diện tích, chu vi hoặc chiều cao của hình thang. Việc nhận diện đúng các cạnh đáy, chiều cao và cạnh bên là bước đầu tiên để áp dụng công thức chính xác.
Lập luận và suy luận dựa trên tính chất hình thang
Phương pháp lập luận thích hợp với các bài toán yêu cầu chứng minh hình thang có tính chất đặc biệt hoặc tìm mối quan hệ giữa các góc, cạnh, và đường chéo. Các tính chất hình học cơ bản của hình thang là nền tảng của phương pháp này.
Các định lý hình học như định lý Pythagore hoặc tính chất về góc bổ sung có thể áp dụng để suy ra chiều cao hoặc các cạnh còn thiếu trong bài toán. Khi giải các bài toán phức tạp, phương pháp này giúp biến đổi, phân tích để sử dụng các định lý phù hợp.

Giải đáp thắc mắc khi giải toán về hình thang
Đối với những bạn bắt đầu học về hình thang, thường sẽ có rất nhiều thắc mắc. KidsUP đã tổng hợp và giải đáp một số thắc mắc như sau:
– Công thức tính chiều cao hình thang
Để tính chiều cao của hình thang, bạn có thể sử dụng công thức: h = 2Sa + b
– Đường trung bình của hình thang là đường nào trong hình?
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Đường trung bình có tính chất là song song với hai cạnh đáy và có độ dài bằng trung bình cộng của hai cạnh đáy.
Công thức tính đường trung bình: a + b2 ( a và b là chiều dài của 2 cạnh đáy)
Có công thức tính thể tích hình thang không?
Hình thang là một hình phẳng trong mặt phẳng hai chiều, nên không có thể tích mà chỉ có diện tích. Công thức tính thể tích chỉ áp dụng cho các hình khối ba chiều như hình hộp, hình lăng trụ, hay hình chóp.
Kết luận
Thông qua bài viết trên, KidsUP đã chia sẻ với bạn toàn bộ những thông tin quan trọng khi học hình thang. Đây là một trong những hình học quan trọng của toán học nên việc hiểu rõ công thức là điều cần thiết. Bạn đừng quên kết hợp giữa lý thuyết và thực hành để bé nắm rõ bài hơn nhé!













