Hình thoi là một trong những tứ giác cơ bản mà trẻ sẽ được học trong chương trình toán tiểu học. Những đặc điểm tính chất, dấu hiệu nhận biết liên quan đến hình này là nội dung cơ bản mà trẻ cần nắm được để hình thành tư duy toán học cũng như tạo nền tảng cho quá trình học tập sau này. Vây hình thoi là gì? Cách tính diện tích, chu vi của hình thoi? Mời mọi người hãy cùng KidsUP tìm hiểu những điều đó qua bài viết dưới đây nhé!
Hình thoi là gì?
Hình thoi là một dạng hình học cơ bản, được định nghĩa là “tứ giác có 4 cạnh bằng nhau, trong đó 2 cạnh đối song song với nhau”. Hay cũng có thể hiểu hình thoi là hình bình hành có 2 cạnh kề bằng nhau, hình bình hành có 2 đường chéo vuông góc với nhau.
Trường hợp hình thoi có 4 góc vuông thì đó là hình vuông. Như vậy, chúng ta có thể hiểu, hình vuông là một trường hợp đặc biệt của hình thoi. Từ đây, chúng ta có kết luận như sau:
- Mọi hình vuông đều là hình thoi nhưng không phải tất cả hình thoi đều là hình vuông.
- Mọi hình thoi đều là hình bình hành nhưng không phải tất cả hình bình hành đều là hình thoi.
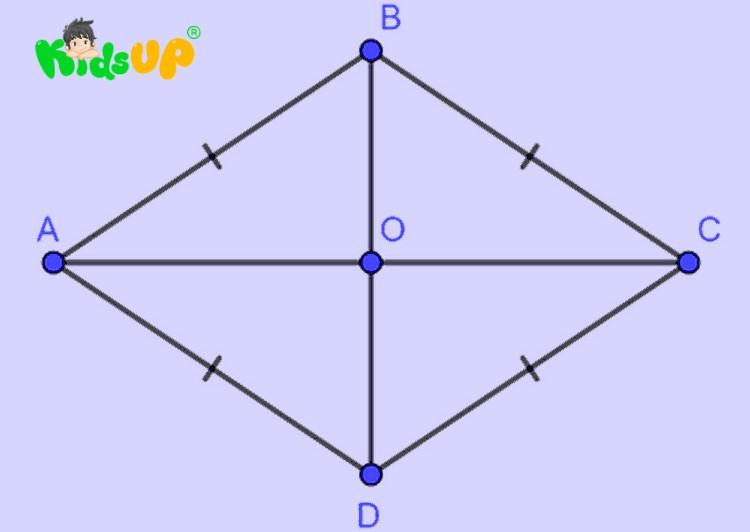
Ngoài định nghĩa hình thoi là gì, trẻ cũng cần phải biết tính chất hình thoi để áp dụng vào các bài tập hình học. Vì là một hình mang tính đối xứng nên hình thoi có một số tính chất đặc trưng như:
- Tất cả 4 cạnh của hình thoi đều có chiều dài bằng nhau.
- Các góc đối diện của hình luôn bằng nhau.
- Hai đường chéo là đường phân giác của các góc trong, vừa là trục đối xứng của hình thoi vuông góc với nhau tại trung điểm của mỗi đường.
- Ngoài ra, hình thoi mang tất cả tính chất của hình bình hành.
Các đặc trưng trên cũng là những dấu hiệu nhận biết hình thoi mà trẻ nên dựa vào những ý đó để giải các bài toán suy luận.
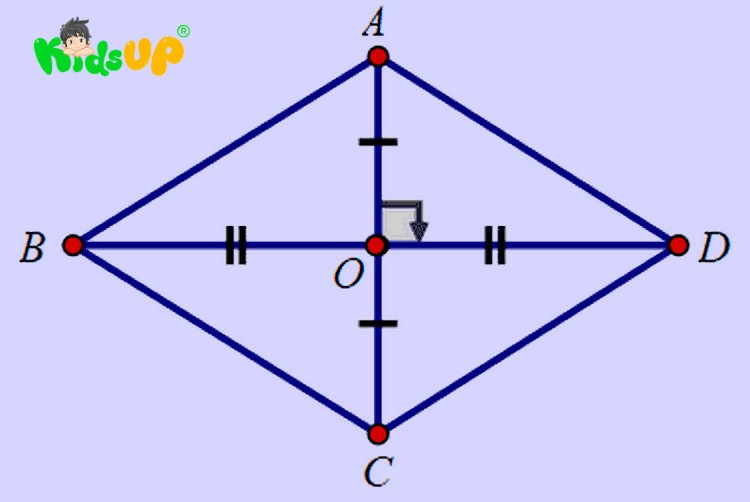
Công thức tính hình thoi chi tiết
Sau khi đã hiểu được định nghĩa, tích chất hình thoi, trẻ cần biết cách tính diện tích, chu vi của hình. Đây là những công thức đơn giản mà trẻ cần nắm được để áp dụng vào các bài tập sau này.
Công thức tính diện tích hình thoi
Cách tính chu vi hình thoi chính là tính tổng độ dài các cạnh bao quanh hình và cũng chính bằng độ dài một cạnh nhân với 4.
Theo đó, công thức tính chu vi hình thoi là: P = a x 4 (với “P” là chu vi hình thoi và “a” là chiều dài cạnh).
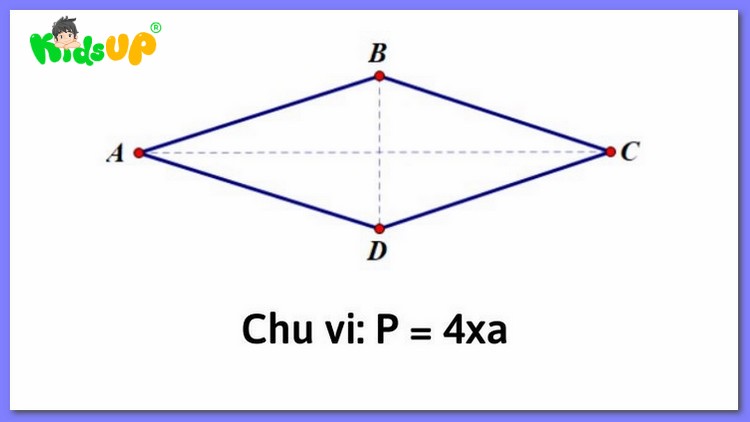
Công thức tính chu vi hình thoi
Diện tích hình thoi là diện tích của phần mặt phẳng mà ta có thể nhìn thấy và được tính bằng một nửa tích chiều dài 2 đường chéo.
Theo đó, công thức tính diện tích hình thoi dựa trên độ dài hai đường chéo là: S = ½ x d1 x d2 = h x a
Với: S: là điện tích của hình thoi
d1, d2 là chiều dài của 2 đường chéo
h là chiều cao hình thoi
a là chiều dài cạnh của hình
Bài tập hình thoi kèm lời giải
So với các dạng hình học khác, hình thoi có nhiều tính chất và cách tính chu vi, diện tích phức tạp hơn đôi chút. Do đó, để trẻ hiểu và ghi nhớ, phụ huynh cần đưa thêm bài tập và ví dụ minh họa. Dưới đây là một số bài tập đơn giản mà bạn có thể tham khảo để hướng dẫn cho trẻ.
Bài tập ứng dụng cách tính diện tích hình thoi
Bài tập 1: Tính diện tích hình thoi dựa trên độ dài 2 đường chéo cho trước.
Bài tập: Tính diện tích hình thoi có đường chéo d1 = 5cm, đường chéo d2 = 8cm.
Lời giải: Áp dụng công thức, ta có diện tích hình thoi = ½ (d1 x d2) = ½ (5 x 8) = 20cm2.
Bài tập 2: Tính diện tích khi chỉ biết chu vi và độ dài một đường chéo.
Bài tập: Tính diện tích hình thoi ABCD khi biết chu vi là 20cm và đường chéo BD dài 6cm.
Lời giải:
Từ công thức tính chu vi P = a x 4 = 20cm, suy ra 1 cạnh AB = 5cm.
Áp dụng định lý Pythagore cho tam giác vuông được tạo nên bởi 2 đường chéo và 1 cạnh. Ta có, AB2 = (AC/2)2 + (BD/2)2 từ đó tìm ra được AC = 4cm.
Áp dụng công thức, ta có diện tích hình thoi ABCD = ½ x AC x BD = 12cm2
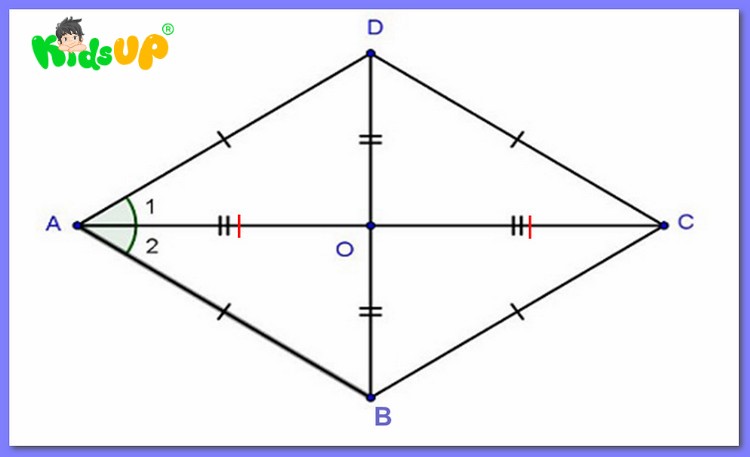
Bài tập tính chu vi hình thoi
Bài tập 1: Tính chu vi hình thoi khi biết độ dài cạnh.
Bài tập: Tính chu vi của hình thoi biết một cạnh có chiều dài bằng 5cm.
Lời giải: Áp dụng công thức tính chu vi, ta có của hình thoi = a x 4 = 5 x 4 = 20cm.
Bài tập 2: Tìm chu vi khi chỉ biết diện tích và độ dài một đường chéo.
Bài tập: Tính chu vi hình thoi khi biết diện tích bằng 24cm2 và đường chéo dài 8cm.
Lời giải:
Từ công thức tính diện tích S = ½ x d1 x d2 ta có 24 = ½ x 8 x d2, từ đó tính được d2 (chiều dài đường chéo còn lại) = 6cm.
Áp dụng định lý Pythagore cho tam giác vuông được tạo từ 1 cạnh và 2 đường chéo ta có:
a2 = (½ d1)2 + (½ d2)2 từ đó suy ra a = 5cm.
Chu vi hình thoi = a x 4 = 5 x 4 = 20cm.
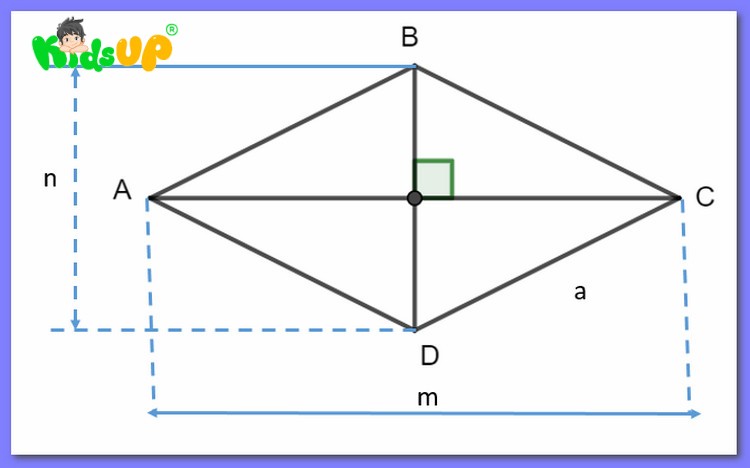
Cách giải bài tập hình thoi nâng cao
Phương pháp tính hình thoi khi biết một số yếu tố
Khi không biết đủ tất cả các yếu tố để tính diện tích, chu vi chúng thì ta cần tìm được chiều dài cạnh và đường chéo. Khi đó, bạn dựa vào tính chất 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường của hình thoi. Hai đường chéo tạo ra 4 tam giác vuông bằng nhau với các cạnh lần lượt là a, 1/2d1 và 1/2d2.
Trong đó:
- a là cạnh huyền tam giác vuông và cũng là cạnh hình thoi.
- 1/2d1 là chiều dài cạnh góc vuông và là 1 nửa chiều dài đường chéo d1.
- 1/2d2 là chiều dài cạnh góc vuông còn lại và là 1 nửa chiều dài đường chéo d2.
Sau đó, áp dụng định lý Pythagore, chúng ta có được công thức a2 = (½ d1)2 + (½ d2)2. Dựa vào đây bạn có thể tính ra cạnh, chiều dài của một đường chéo khi đã biết 2 yếu tố còn lại.
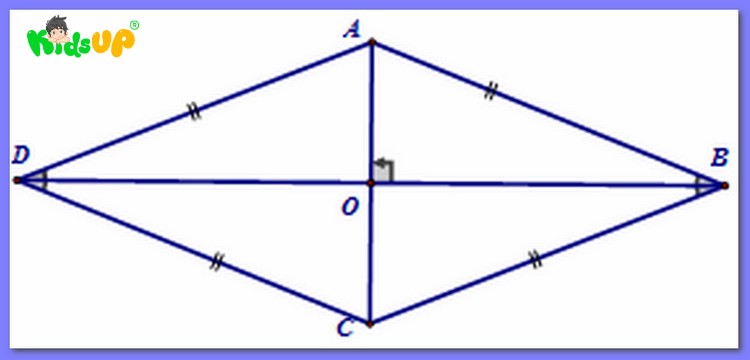
Các mẹo giải nhanh bài tập về hình thoi
Để giải nhanh các bài tập về hình thoi, phụ huynh có thể áp dụng một số mẹo sau cho trẻ:
- Vẽ hình để dễ dàng quan sát các cạnh, đường chéo.
- Từ công thức tính chu vi, diện tích để suy luận tìm ra chiều dài canh, đường chéo khi đã biết các yếu tố còn lại.
- Áp dụng tích chất đặc biệt của hình tam giác vuông, hình bình hành khi cần thiết.
Định nghĩa, tính chất, cách tính diện tích, chu vi của hình thoi đều đã được KidsUP trình bày ở bài viết trên. Đây là một dạng hình học cơ bản mà trẻ cần phải nắm chắc kiến thức để áp dụng vào những chương trình học sau này. Do đó, phụ huynh cần để trẻ thường xuyên nhắc lại, làm bài tập liên quan để ghi nhớ, hiểu rõ bản chất của hình thoi.













