Hình tròn là một hình học cơ bản, xuất hiện khắp nơi trong cuộc sống. Bạn có thể bắt gặp hình học này qua hình dáng cái đồng hồ, chiếc bánh,…Để có thể hiểu biết các đặc điểm của hình này, bạn cần nắm rõ kiến thức về việc tính chu vi và diện tích. Trong bài viết sau đây, KidsUP sẽ tổng hợp toàn bộ kiến thức từ A đến Z về hình tròn dành cho học sinh lớp 3, giúp các em tự tin hơn trong học tập và ứng dụng vào thực tế.
Định nghĩa và đặc điểm cơ bản của hình tròn
Hình tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng cách đều một điểm cố định, được gọi là tâm của hình. Khoảng cách từ tâm đến mỗi điểm trên đường viền của hình tròn được gọi là bán kính. Đường viền của hình tròn được gọi là đường tròn.
Hình tròn có tính chất nổi bật là mọi điểm trên đường tròn đều cách đều tâm, tạo thành một khoảng cách cố định gọi là bán kính. Nhờ đặc điểm này, hình tròn luôn giữ được sự đồng đều, không có điểm nào trên viền vượt trội hoặc khác biệt về khoảng cách so với các điểm khác.
Sự đối xứng và tính liên tục của hình tròn:
- Sự đối xứng: Hình tròn có tính đối xứng hoàn hảo qua tâm. Bất kỳ đường kính nào, khi kẻ qua tâm, cũng đều chia hình tròn thành hai phần bằng nhau.
- Tính liên tục: Đường viền của hình tròn là một đường cong khép kín, không có điểm đầu và điểm cuối, tạo nên tính liên tục và không ngắt quãng.
Các yếu tố cơ bản của hình tròn lớp 3
Hình tròn là một trong những hình quan trọng của chương trình lớp 3. Do đó, bé cần phải nắm rõ các yếu tố cơ bản của hình tròn như sau:
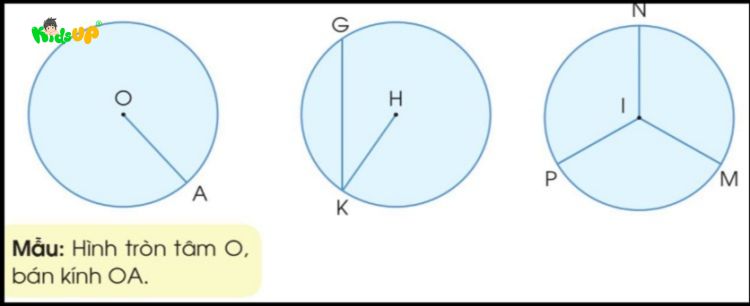
Tâm của hình tròn
Tâm của hình tròn là điểm nằm chính giữa, cách đều tất cả các điểm trên đường viền của hình tròn. Tâm thường được ký hiệu là chữ “O”.
Để xác định tâm, ta có thể dùng một dụng cụ như compa để vẽ hình tròn, trong đó đầu kim của compa là tâm của hình tròn. Nếu đường tròn đã có sẵn, bạn tìm tâm bằng cách vẽ hai hoặc nhiều đường kính. Điểm giao nhau của các đường kính trong hình tròn chính là tâm.
Tâm đóng vai trò quan trọng trong các phép đo và tính toán liên quan đến hình tròn:
- Đo bán kính: Bán kính là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn. Độ dài bán kính là thông số cơ bản để tính chu vi và diện tích của hình tròn.
- Đo đường kính: Đường kính là đoạn thẳng đi qua tâm và có hai đầu nằm trên đường tròn. Đường kính gấp đôi bán kính và cũng là yếu tố quan trọng trong các phép tính liên quan đến hình tròn.
- Tính chu vi và diện tích: Tâm giúp xác định bán kính và đường kính, từ đó dùng để tính chu vi và diện tích hình tròn dựa trên công thức có liên quan đến bán kính.
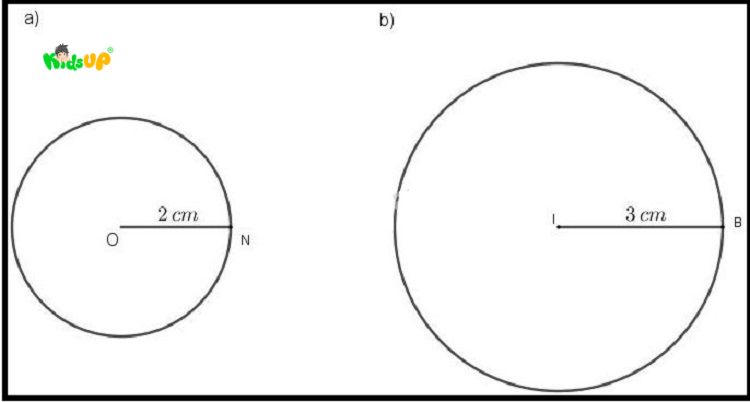
Bán kính (R) của hình tròn
Bán kính của hình tròn, ký hiệu là R, là khoảng cách từ tâm của hình tròn đến bất kỳ điểm nào trên đường tròn. Để đo bán kính, ta cần xác định chính xác tâm của hình tròn, sau đó đo khoảng cách từ tâm đến một điểm bất kỳ nằm trên viền hình tròn. Nếu có một đoạn thẳng nối từ tâm đến viền, thì chiều dài của đoạn này chính là bán kính.
Ứng dụng của bán kính:
- Xây dựng và thiết kế: Bán kính thường được dùng trong kiến trúc và kỹ thuật để xác định kích thước của các bề mặt tròn. Ví dụ như thiết kế cầu thang xoắn ốc, các mặt đường, các bộ phận máy móc có hình tròn,…
- Ứng dụng trong cuộc sống: Bán kính còn được ứng dụng trong việc tính toán các kích thước tròn trong đời sống. Ví dụ như tính chu vi bể bơi, bàn tròn,…
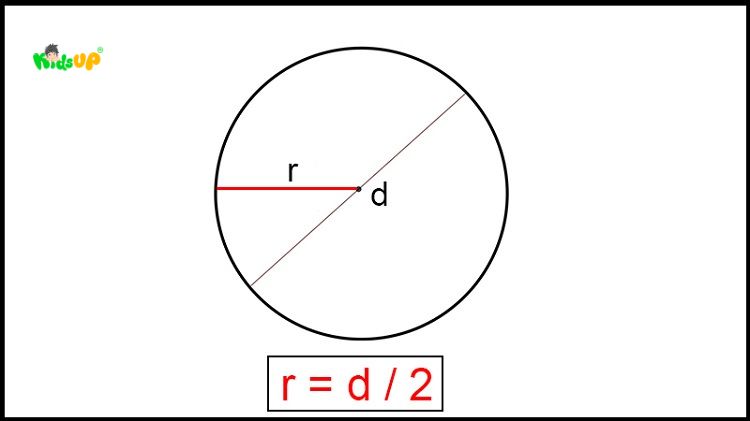
Đường kính (D) của hình tròn
Đường kính hình tròn, ký hiệu là D, là đoạn thẳng đi qua tâm và có hai đầu nằm trên đường tròn. Để đo đường kính, bé cần xác định tâm của hình tròn trước, sau đó chọn hai điểm nằm trên viền sao cho đoạn thẳng nối hai điểm này đi qua tâm. Khoảng cách giữa hai điểm này chính là chiều dài của đường kính.
Đường kính có chiều dài luôn gấp đôi bán kính. Công thức liên hệ giữa đường kính và bán kính là: D = 2 x R.
Vì chu vi của hình tròn có công thức C=2 × π ×R. Bạn có thể thay thế bán kính bằng nửa đường kính, từ đó cũng có thể viết lại công thức chu vi dựa vào đường kính: C= π×D.
Công thức tính toán của hình tròn
Có những công thức tính toán nào liên quan đến hình tròn? Bạn hãy cùng bé tìm hiểu các công thức tính sau đây nhé!
Công thức tính diện tích hình tròn
Diện tích của hình tròn chính là toàn bộ không gian bên trong đường tròn. Để tính diện tích hình tròn, ta sử dụng công thức: A= π × R2
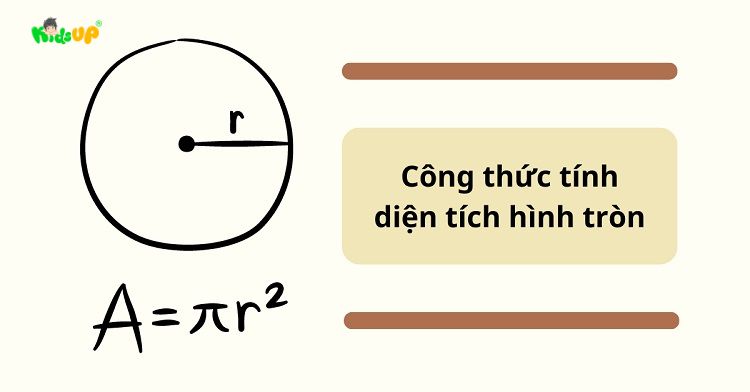
Trong đó:
- A là diện tích hình tròn.
- π là hằng số, xấp xỉ bằng 3.14159.
- R là bán kính của hình tròn.
Công thức tính chu vi hình tròn
Chu vi của hình tròn là chiều dài của đường viền bao quanh hình tròn. Công thức tính chu vi được xác định như sau: C= 2 × π × R hoặc C = π × D
Trong đó:
- C là chu vi của hình tròn.
- π là hằng số, xấp xỉ bằng 3.14159.
- R là bán kính của hình tròn.
- D là đường kính của hình tròn
Cách nhận biết và vẽ hình tròn lớp 3
Làm thế nào để nhận biết và vẽ hình tròn lớp 3? Sau đây là những cách mà ba mẹ có thể hướng dẫn bé để có thể vẽ hình tròn tại nhà chính xác:
Dụng cụ và cách vẽ hình tròn
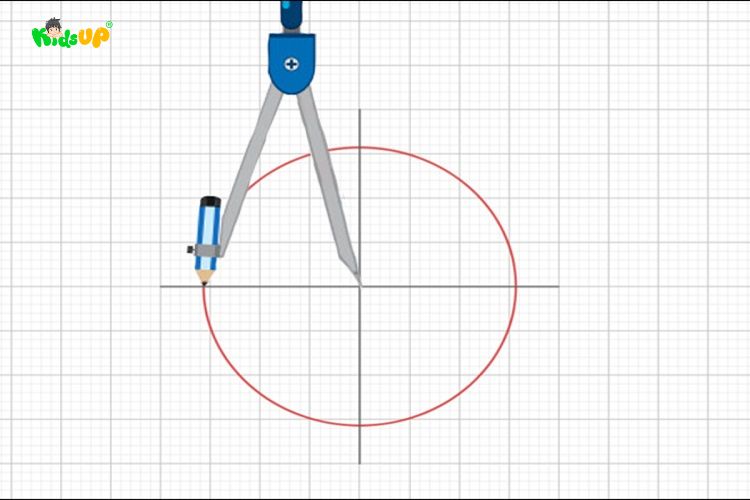
Bạn nên chuẩn bị compa, bút chì và một tờ giấy trắng. Sau đó, bạn sẽ hướng dẫn sử dụng compa để vẽ hình tròn:
- Bước 1: Chuẩn bị một chiếc compa và đặt một cây bút chì vào chân có khe giữ bút.
- Bước 2: Xác định tâm của hình tròn mà bạn muốn vẽ và đặt đầu kim của compa vào điểm này.
- Bước 3: Điều chỉnh khoảng cách giữa đầu kim và bút chì sao cho bằng bán kính mong muốn.
- Bước 4: Giữ chắc đầu kim ở tâm và xoay nhẹ nhàng compa một vòng tròn, để bút chì vẽ trên giấy.
Mẹo vẽ hình tròn chuẩn không cần compa:
- Dùng một đồng xu hoặc nắp chai: Chọn một vật tròn có kích thước phù hợp, bé đặt lên giấy và dùng bút chì vẽ theo đường viền của vật tròn.
- Sử dụng dây hoặc sợi chỉ: Bạn cắt một đoạn dây dài bằng bán kính hình tròn cần vẽ. Sau đó, bạn giữ một đầu dây cố định tại tâm, đầu còn lại buộc bút chì. Giữ chắc đầu dây ở tâm và kéo căng bút chì để vẽ xung quanh, tạo thành một hình tròn.
Nhận biết hình tròn trong các hình dạng khác
Cách nhận biết hình tròn với những hình khác:
- Hình tròn: Là một hình có tất cả các điểm trên viền cách đều một điểm duy nhất (tâm), tạo nên một đường cong đều và khép kín. Đặc điểm nổi bật của hình tròn là tính đối xứng qua mọi đường kính và khoảng cách từ tâm đến viền là không đổi (bán kính).
- Hình oval: Là một đường cong khép kín nhưng không đều. Khoảng cách từ một điểm bất kỳ trên viền đến tâm của hình không đồng nhất. Hình oval có chiều dài và chiều rộng khác nhau, không đối xứng hoàn toàn như hình tròn.
- Hình đa giác: Hình đa giác là hình có các cạnh thẳng, không phải là đường cong liên tục như hình tròn. Ví dụ, hình tam giác, tứ giác, lục giác đều có các cạnh thẳng nối với nhau.
Các bài toán cơ bản về hình tròn lớp 3
Một trong những cách để giúp bé học kiến thức về hình tròn dễ nhớ chính là thông qua việc làm bài tập. Sau đây là các bài toán cơ bản về hình tròn lớp 3 mà bạn có thể tham khảo để hướng dẫn bé:
Bài toán tính chu vi hình tròn
Bài 1: Tính chu vi của hình tròn có bán kính R = 7 cm.
Lời giải: Chu vi hình tròn là: C = 2 × π × R = 2 x 3.14 x 7 = 43.96 cm.
Bài 2: Tính chu vi của hình tròn có đường kính D = 10 cm
Lời giải: Chu vi hình tròn là: C = 2 × π × R = π x D = 31.4 cm
Bài toán tìm diện tích hình tròn
Bài 1: Tính diện tích của hình tròn có bán kính R = 5 cm.
Lời giải: Áp dụng công thức tính diện tích: A= π × R2 = 3.14 × 522 = 78.5 cm2
Bài 2: Tính diện tích của hình tròn có đường kính D = 20 cm.
Lời giải:
- Bán kính hình tròn là: R = D : 2 = 20 : 2 = 10
- Diện tích hình tròn là: A= π × R2 = 3.14 x 102 = 314 cm2

Bài toán tìm đường kính và bán kính hình tròn
Dạng 1: Tìm đường kính đường tròn khi cho chiều dài bán kính
Mối liên hệ giữa đường kính và bán kính: D=2 x R, trong đó:
- D là đường kính,
- R là bán kính.
Đề bài: Một hình tròn có bán kính R = 6 cm. Tính đường kính hình tròn.
Lời giải: Đường kính của hình tròn là: D = 2 x R = 2 x 6 = 12 cm.
Dạng 2: Tìm bán kính khi biết chu vi
Công thức chu vi hình tròn C = 2 x π x R => R = C 2 x
Đề bài: Một hình tròn có chu vi là 31.4 cm. Tìm bán kính của hình tròn.
Lời giải: Bán kính của hình tròn là: R = C 2 x = 31.4 2 x 3.14 = 5cm
Dạng 3: Tìm bán kính khi biết diện tích
Công thức tính diện tích của hình tròn là A= π × R2 => R = A
Đề bài: Một hình tròn có diện tích là 78.5 cm2. Tìm bán kính của hình tròn.
Lời giải: Bán kính của hình tròn là: R = A = 78.53.14 = 25 = 5 cm
Kết luận
Bài viết trên là những nội dung tổng hợp kiến thức về hình tròn và những công thức tính toán về chu vi, diện tích. Mong rằng với những kiến thức mà KidsUP chia sẻ phía trên sẽ giúp ích cho trẻ trong quá trình học môn toán tiểu học.













