Trong môn toán hình học lớp 2, một trong những hình học cơ bản mà các em sẽ được học là hình tứ giác. Vậy hình tứ giác là gì? Chúng có những đặc điểm nào nổi bật và làm sao để tính chu vi cũng như diện tích hình này? Hãy cùng KidsUP khám phá kiến thức về hình tứ giác lớp 2, tìm hiểu các tính chất cơ bản và cách tính toán chu vi và diện tích một cách dễ dàng nhé!
Định nghĩa hình tứ giác là gì?
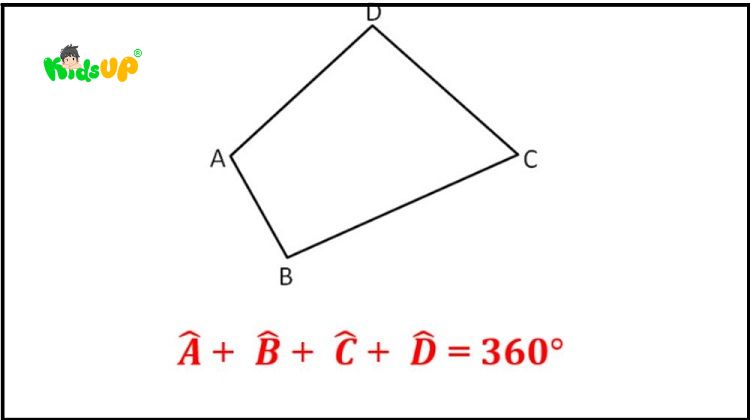
Hình tứ giác là một hình học phẳng có bốn cạnh và bốn đỉnh, tạo thành từ bốn đoạn thẳng nối liền nhau. Tổng số đo các góc trong của một hình tứ giác luôn bằng 360 độ.
Đặc điểm của hình tứ giác là hình như thế nào:
- Có 4 cạnh: Các cạnh có thể có độ dài khác nhau.
- Có 4 góc: Tổng các góc bên trong luôn bằng 360 độ.
- Có 4 đỉnh: Các điểm giao nhau giữa các cạnh với nhau gọi là đỉnh của tứ giác.
- Không có cạnh nào cắt nhau: Tất cả các cạnh nối liền với nhau để tạo thành một hình khép kín.
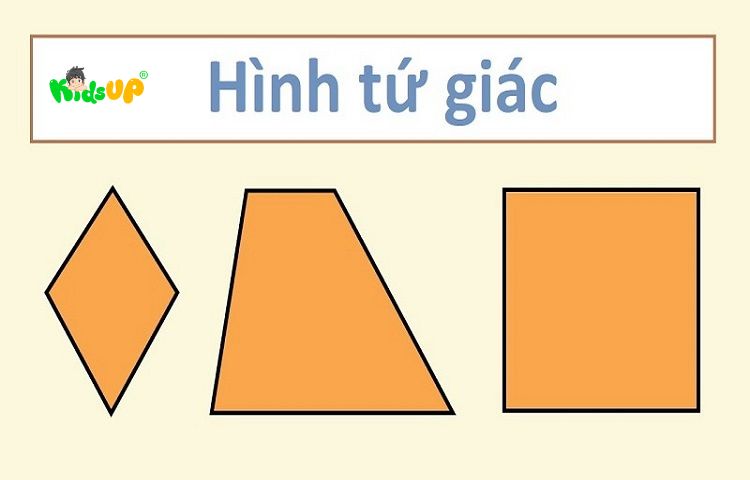
Một số loại hình tứ giác thường gặp trong toán lớp 2:
- Hình vuông: Hình có 4 góc vuông, mỗi góc 90 độ và 4 cạnh bằng nhau.
- Hình chữ nhật: Hình có 4 góc vuông, 2 cặp cạnh đối song song và bằng nhau.
- Hình thang: Hình có 1 cặp cạnh đối nhau, song song, 4 góc là 360 độ.
- Hình bình hành: Hình có 2 cặp cạnh bằng nhau và song song với nhau.
- Hình thoi: Có 2 cặp cạnh đối song song và 4 cạnh bằng nhau.
Tính chất hình tứ giác
Tùy theo từng loại hình tứ giác mà tính chất của các hình đó sẽ có sự khác biệt. Việc nắm rõ tính chất của từng hình sẽ giúp cho bé dễ dàng thực hiện các phép toán tính chu vi và diện tích của từng hình.
Tính chất chung của các hình tứ giác
Hình tứ giác có nhiều tính chất chung mà bé cần hiểu rõ để có thể tính toán và áp dụng trong hình học. Dưới đây là những tính chất chung của các loại hình tứ giác:
Tổng số đo các góc trong của bất kỳ hình tứ giác nào cũng luôn bằng 360 độ. Ví dụ như trong một hình có 4 góc 90 độ thì tổng số đo cũng sẽ bằng 360 độ. Ngoài ra, hình còn có tính chất đối xứng, cụ thể:
- Đối xứng trục: Một số loại tứ giác như hình vuông, hình chữ nhật, hình thoi có trục đối xứng. Nghĩa là, khi gấp đôi hình theo một đường thẳng nào đó, hai nửa sẽ trùng khít nhau.
- Đối xứng tâm: Một số tứ giác như hình vuông, hình chữ nhật, hình bình hành đối xứng tâm. Đối xứng tâm nghĩa là nếu quay hình quanh một điểm trung tâm 180 độ, hình sẽ trùng khít với chính nó.
Tính chất của từng loại hình tứ giác
Mỗi loại hình tứ giác sẽ có các tính chất khác nhau. Những tính chất này là nền tảng để người học hiểu và giải các bài toán liên quan đến hình tứ giác, đặc biệt khi tính chu vi, diện tích. Bạn có thể tham khảo các tính chất của từng loại hình tứ giác chi tiết sau đây:
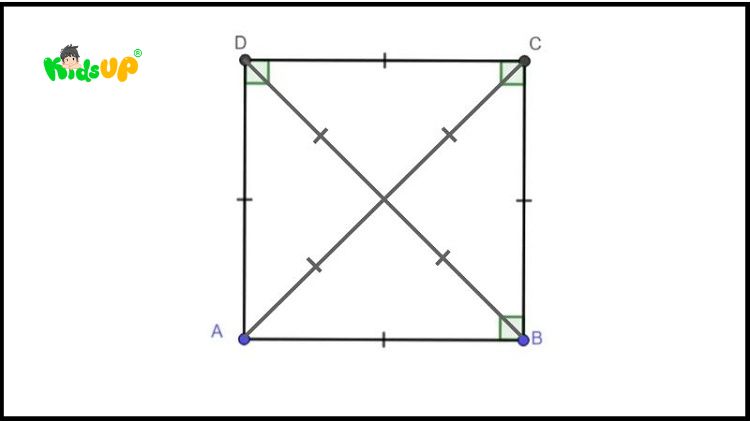
Tính chất của hình vuông:
- Bốn cạnh bằng nhau: Mọi cạnh của hình vuông đều có độ dài bằng nhau.
- Bốn góc vuông: Mỗi góc của hình vuông đều là góc vuông, tức là 90 độ.
- Hai đường chéo bằng nhau và vuông góc với nhau: Hai đường chéo trong hình vuông không chỉ bằng nhau mà còn cắt nhau nhau thành các góc 90 độ.
- Đối xứng trục: Hình vuông có 4 trục đối xứng, tức là có thể gấp lại qua 4 đường thẳng khác nhau mà hai nửa sẽ trùng khít.
- Đối xứng tâm: Hình vuông có đối xứng tâm tại giao điểm của hai đường chéo.
Tính chất của hình chữ nhật:
- Hai cặp cạnh đối bằng nhau và song song: Hình chữ nhật có hai cạnh dài bằng nhau và hai cạnh ngắn bằng nhau.
- Bốn góc vuông: Mỗi góc của hình chữ nhật đều là góc vuông, tức là 90 độ.
- Hai đường chéo bằng nhau: Hai đường chéo của hình chữ nhật có độ dài bằng nhau nhưng không vuông góc với nhau như ở hình vuông.
- Đối xứng trục: Hình chữ nhật có 2 trục đối xứng (theo chiều dài và chiều rộng).
- Đối xứng tâm: Hình chữ nhật có đối xứng tâm tại giao điểm của hai đường chéo.
Tính chất của hình thang:
- Một cặp cạnh đối song song: Hình thang có một cặp cạnh song song, được gọi là đáy.
- Hai góc kề một cạnh bên có tổng bằng 180 độ: Tính chất này áp dụng cho các góc kề với một cạnh bên của hình thang.
- Hình thang cân (một loại hình thang đặc biệt) có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau. Đường chéo của hình thang cân cắt nhau và có độ dài bằng nhau.
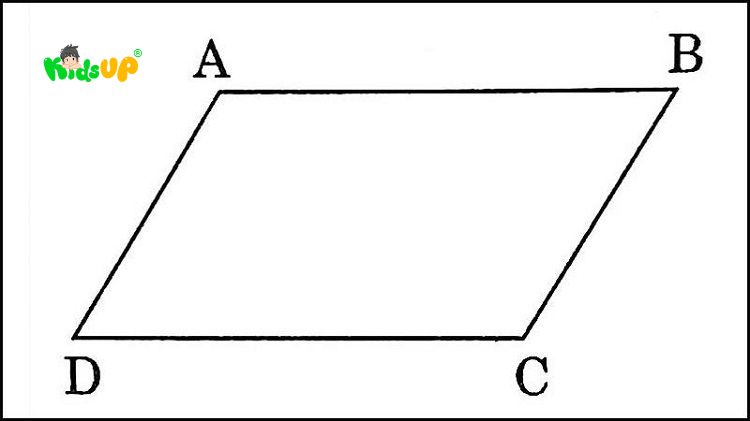
Tính chất của hình bình hành:
- Hai cặp cạnh đối song song và bằng nhau: Các cạnh đối diện của hình bình hành có độ dài bằng nhau và song song với nhau.
- Hai góc đối bằng nhau: Hai góc đối diện của hình bình hành có số đo bằng nhau.
- Hai đường chéo chia nhau tại trung điểm: Hai đường chéo của hình bình hành cắt nhau tại điểm giữa, nhưng chúng không vuông góc với nhau.
- Đối xứng tâm: Đối xứng tâm tại giao điểm của hai đường chéo cắt nhau.
Cách tính chu vi hình tứ giác.
Công thức tổng quát tính chu vi
Cách tính chu vi một hình tứ giác bất kỳ chính là cộng tổng độ dài 4 cạnh của hình lại với nhau. Công thức này có thể áp dụng cho mỗi loại hình tứ giác, kể cả những hình độ dài các cạnh không bằng nhau.
Nếu gọi các độ dài của các cạnh lần lượt là a, b, c, d, thì chu vi sẽ là: a + b + c + d. Để có thể áp dụng công thức này, bé cần biết chính xác độ dài của các cạnh.
Cách tính chu vi của từng loại hình tứ giác
Tùy theo tính chất của từng hình mà công thức tính chu vi hình tứ giác sẽ có sự khác biệt. Cụ thể:
- Chu vi hình vuông: Vì hình vuông có bốn cạnh bằng nhau nên nếu cạnh của hình vuông là a. Công thức tính chu vi là: 4 x a.
- Chu vi hình chữ nhật: Gọi a là chiều dài còn b là chiều rộng của hình chữ nhật. Công thức tính chu vi: ( a + b ) x 2.
- Chu vi hình thang: Gọi a và b lần lượt là chiều dài của 2 đáy, c và d là 2 cạnh bên. Công thức tính chu vi hình thang: a + b + c + d.
- Chu vi hình bình: Gọi a là cạnh dài, b là cạnh ngắn hình chữ nhật. Công thức tính chu vi: ( a + b ) x 2.

Cách tính diện tích hình tứ giác
Diện tích của hình tứ giác là phần không gian được bao phủ bởi bốn cạnh của hình đó trên một mặt phẳng. Nói cách khác, công thức tính diện tích hình tứ giác là là để tính ra số đo phần mặt phẳng nằm bên trong đường bao bốn cạnh của hình tứ giác. Bạn có thể hướng dẫn bé học tính diện tích của từng loại hình tứ giác sau đây:
Diện tích hình vuông
Gọi a là cạnh của hình vuông bất kỳ, công thức tính diện tích hình vuông: a x a
Bài tập: Một hình vuông có cạnh dài 5 cm. Bé cần tính diện tích của hình vuông.
Lời giải: Diện tích của hình vuông là: 5 x 5 = 25 cm2
Diện tích hình chữ nhật
Gọi a là chiều dài, còn b là chiều rộng của hình chữ nhật. Công thức tính diện tích: a x b.
Bài tập: Một hình chữ nhật có chiều dài là 3 cm, chiều rộng là 5 cm. Bé hãy tính diện tích của hình chữ nhật trên.
Lời giải: Diện tích của hình chữ nhật là: 3 x 5 = 15 cm2
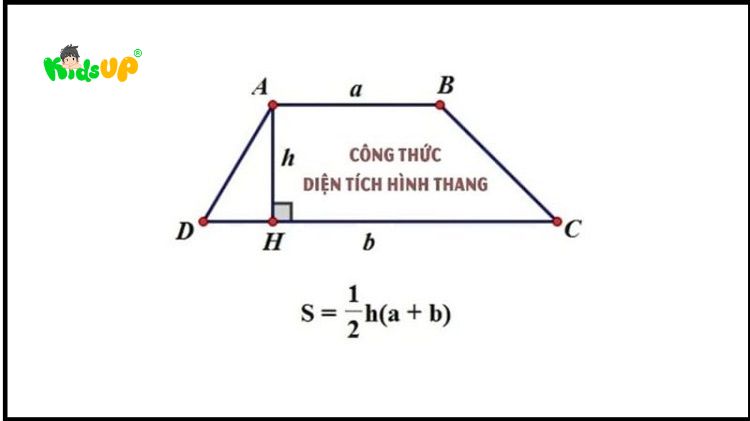
Diện tích hình thang
Gọi a và b lần lượt là chiều dài của 2 đáy, và h là chiều cao của hình thang. Công thức tính diện tích: 12 x (a+b) x h.
Bài tập: Một hình thang có đáy lớn 10 cm, đáy nhỏ 6 cm và chiều cao 4 cm. Tính diện tích của hình thang.
Lời giải: Diện tích của hình thang là: 12 x ( 10 + 6 ) x 4 = 32 cm2
Diện tích hình bình hành
Gọi a là chiều dài của cạnh đáy, h là chiều cao. Công thức tính diện tích: a x h.
Bài tập: Một hình bình hành có cạnh đáy dài 7 cm, chiều cao 5 cm. Tính diện tích hình bình hành.hình tứ giác là hình như thế nào
Lời giải: Diện tích hình bình hành là: 7 x 5 = 35 cm2
Kết luận
Qua bài viết trên, KidsUP đã chia sẻ tới ba mẹ và các bạn học sinh những kiến thức và công thức căn bản về hình tứ giác lớp 2. Mong rằng cách chia sẻ của chúng tôi sẽ giúp các bạn học sinh nắm được những kiến thức về hình học này một cách nhanh chóng.













